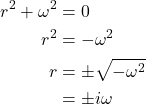I. Derivation of Wave Equation
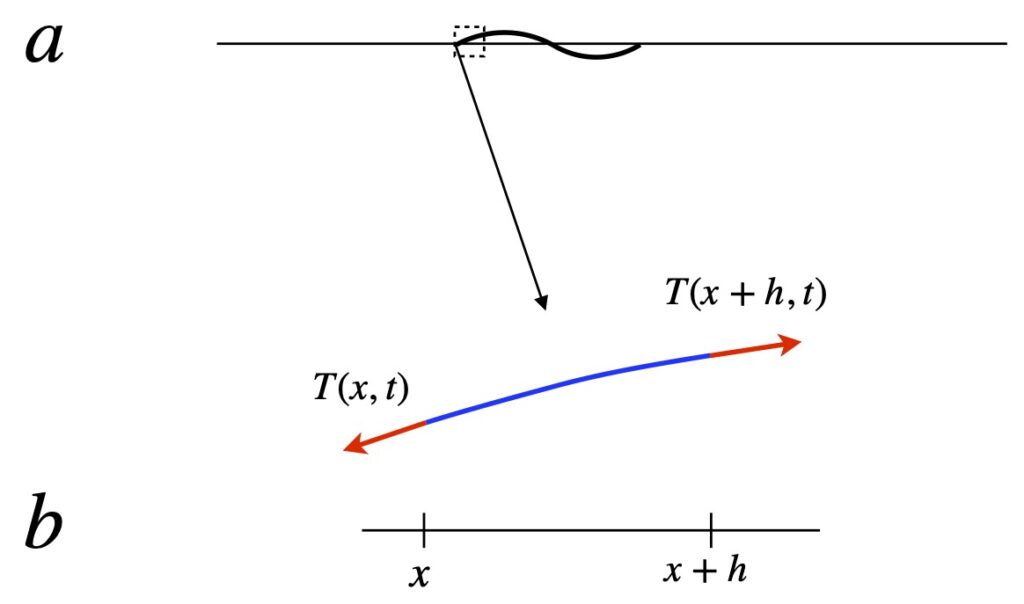
We wish to derive the wave equation. Consider figure 1 above. Figure 1a shows a string fixed at both ends. We tweak the string at its lefthand margin and cause a wave to propagate to the right along the string. Figure 1b is a blow up of the tiny string segment shown in the dotted square in figure 1a. We make 4 assumptions for our derivation:
- Motion of the string is only vertical
- The string offers no resistance to bending (If it did, there would be horizontal force components and the only horizontal force components we want to consider are those caused by tension in the string)
- The height of the string’s vibration is small
- The density in the tiny string segment we’re considering in figure 1b is uniform
We’ll start our derivation by with Newton’s second law of motion:
![]()
Let’s look at acceleration, ![]() , first. The acceleration with which we’re concerned is in the up-down direction, the only direction in which the string moves. We’ll designate that direction
, first. The acceleration with which we’re concerned is in the up-down direction, the only direction in which the string moves. We’ll designate that direction ![]() . We know from classical mechanics that acceleration is the second derivative of displacement. The acceleration, in this case, is:
. We know from classical mechanics that acceleration is the second derivative of displacement. The acceleration, in this case, is:
![]()
where ![]() is the second partial derivative of the up-down displacement,
is the second partial derivative of the up-down displacement, ![]() .
.
Next, let’s consider the mass, ![]() of the tiny string segment from x to x + h. This is given by the mass density (mass per unit length),
of the tiny string segment from x to x + h. This is given by the mass density (mass per unit length), ![]() , of the string segment times the length of that segment:
, of the string segment times the length of that segment: ![]() . We’ll assume that the density over such a small string segment is uniform. Therefore, we can use the density at any point along the segment to find the mass. Let’s choose
. We’ll assume that the density over such a small string segment is uniform. Therefore, we can use the density at any point along the segment to find the mass. Let’s choose ![]() . For the length, since the amplitude of the string’s vibration is small, it is relatively flat. Therefore,
. For the length, since the amplitude of the string’s vibration is small, it is relatively flat. Therefore, ![]() . So:
. So:
![]()
Now let’s tackle the forces. The only forces that we’ll consider in this article are the forces caused by tension on the string. The tension in the string is tangent to the string. It has 2 components: one in the u-direction and another in the x-direction.
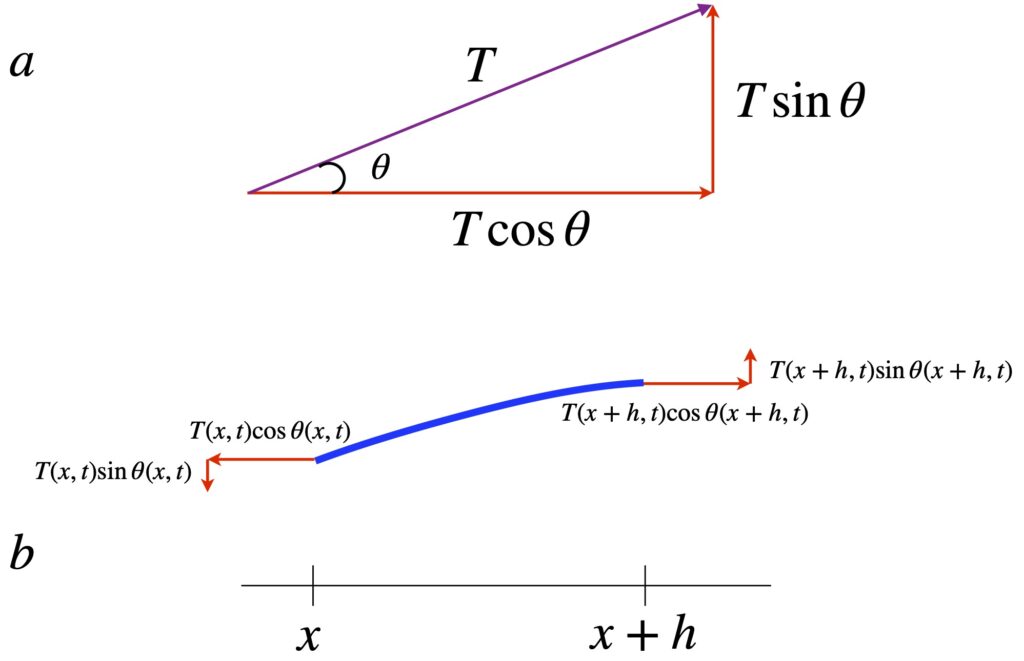
Figure 2a shows how, using trigonometry, that we can calculate the components of force caused by string tension in each direction. Figure 2b depicts the mathematical expressions for force components related to string tension.
Since there’s no horizontal motion of the string, that means that the x-direction of tension coming from ![]() is equal and opposite to the x-direction tension at
is equal and opposite to the x-direction tension at ![]() . Mathematically, as shown in the diagram:
. Mathematically, as shown in the diagram:
![]()
So:
![]()
The more important force to evaluate is that in the u-direction. The force in the upward direction due to ![]() is
is ![]() . That at
. That at ![]() is
is ![]() . The net upward force is:
. The net upward force is:
![]()
Collecting terms, we get what’s shown in figure 3:
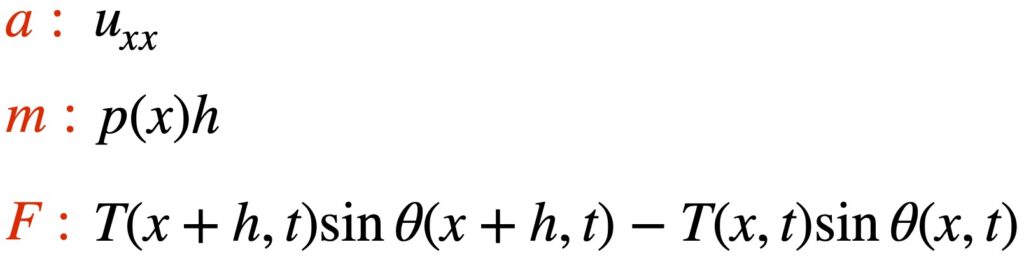
Plugging these values into eq (1.1), we get:
![]()
Next, divide both sides by ![]() :
:
![]()
Take the limit as ![]() on both sides of the equation. This makes the left side of the equation equal to the partial derivative of
on both sides of the equation. This makes the left side of the equation equal to the partial derivative of ![]() with respect to
with respect to ![]() :
:
![]()
We’d like to get rid of the ![]() term and get everything in the equation in terms of
term and get everything in the equation in terms of ![]() . To do this, we note (as depicted in figure 4) that the slope of our string is given by a line to our string at any given point. The slope of this tangent line is
. To do this, we note (as depicted in figure 4) that the slope of our string is given by a line to our string at any given point. The slope of this tangent line is ![]() . But we said at the beginning of this discussion that the tension in the string is always tangent to the string. And as seen in figure 2a, that tension has components
. But we said at the beginning of this discussion that the tension in the string is always tangent to the string. And as seen in figure 2a, that tension has components ![]() and
and ![]() . Therefore:
. Therefore:
![]()
But one of our assumptions was that the magnitude of the string oscillations was small meaning that ![]() . That, in turn, means that
. That, in turn, means that ![]() which means that:
which means that:
![]()
So we can replace ![]() with
with ![]() to get
to get
![]()
So:
![]()
If we make 2 further assumptions:
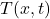 is constant (i.e.,
is constant (i.e., 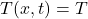 (perfect elasticity))
(perfect elasticity))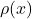 is constant i.e., (
is constant i.e., (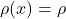 )
)
Then ![]() and
and ![]() can be pulled out of the derivatives. We get:
can be pulled out of the derivatives. We get:
![]()
Eq 1.13 is often expressed as:
![]()
To see why this is the case, let’s examine the units of ![]() . We have:
. We have:
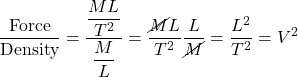
where
![]() is mass
is mass
![]() is length
is length
![]() is time
is time
![]() is velocity (speed, actually) at which the wave propagates
is velocity (speed, actually) at which the wave propagates
Thus, ![]() has units of speed squared. For electromagnetic waves, that speed is c, the speed of light.
has units of speed squared. For electromagnetic waves, that speed is c, the speed of light.
II. Solutions to the Wave Equation
II.1 Transport Equation Method
II.1.1 Transport Equation
Consider a wave moving to the right with constant velocity, as depicted in figure 2.1.1.
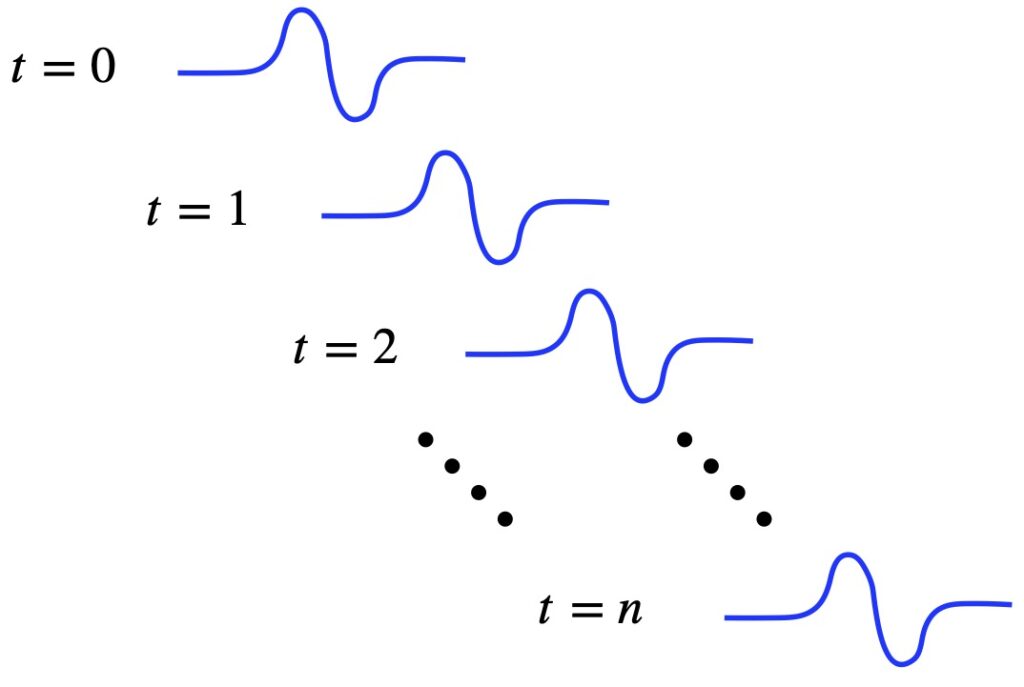
What kind of partial differential equation (pde) would this be a solution to? One like the transport equation, the simplest pde to exhibit such a solution:
![]()
where
![]() ,
, ![]() and
and ![]() are directions in a 3D space
are directions in a 3D space
![]()
![]()
![]() is a constant
is a constant
Let’s look at this from a slightly different perspective (figure 2.1.2):
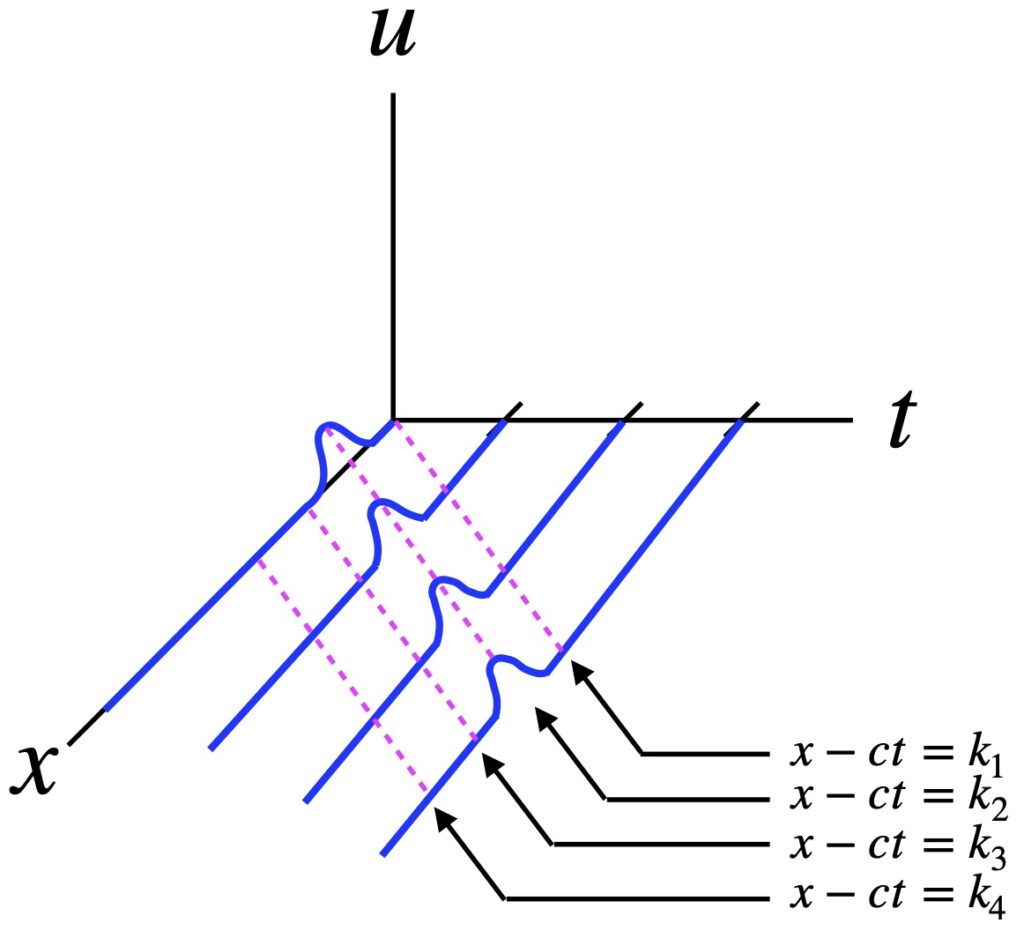
In figure 2.1.2, the blue waves are moving in the x-direction with constant speed, ![]() . Note that the wave amplitude,
. Note that the wave amplitude, ![]() , is constant along the parallel magenta dotted lines which all have the equation
, is constant along the parallel magenta dotted lines which all have the equation ![]() . Such parallel lines are called characteristic lines.
. Such parallel lines are called characteristic lines.
We can think of the blue waves as forming a surface. Recall the concept of the directional derivative from multivariable calculus. Basically, we define a tangent plane to the surface and take the derivative in a particular direction. Mathematically, it’s defined as the inner product of the gradient of a scalar field:
![]()
where
![]() is a vector that points in the direction of the directional derivative
is a vector that points in the direction of the directional derivative
![]() is a scalar field
is a scalar field
![]() is the gradient of the scalar field
is the gradient of the scalar field
As it applies to our case here, we’re taking the directional derivative in the direction of the parallel lines given by ![]() . And since we said that
. And since we said that ![]() does not change along those lines, then the directional derivative is 0.
does not change along those lines, then the directional derivative is 0.
The vector, ![]() , in our case, is given by
, in our case, is given by ![]() since we’re moving
since we’re moving ![]() units in the x-direction in 1 unit of time. The gradient of our scalar field is given by
units in the x-direction in 1 unit of time. The gradient of our scalar field is given by ![]() . Thus, by the definition of the directional derivative, we have:
. Thus, by the definition of the directional derivative, we have:
![]()
which, of course, is the transport equation.
We could also write ![]() as a function of
as a function of ![]() with the x-coordinate being
with the x-coordinate being ![]() which implies that
which implies that ![]() . We know that
. We know that ![]() doesn’t change along the characteristic line so the derivative with respect to time should be zero:
doesn’t change along the characteristic line so the derivative with respect to time should be zero:
![]()
We use the chain rule to take this derivative:
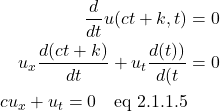
Again, we end up with the transport equation.
Hopefully, that provides some intuition about what the transport equation is. Now we turn our attention to its solution.
II.1.2 Transport Equation Solution
To solve the transport equation, consider the scenario outlined in figure 2.2.1.
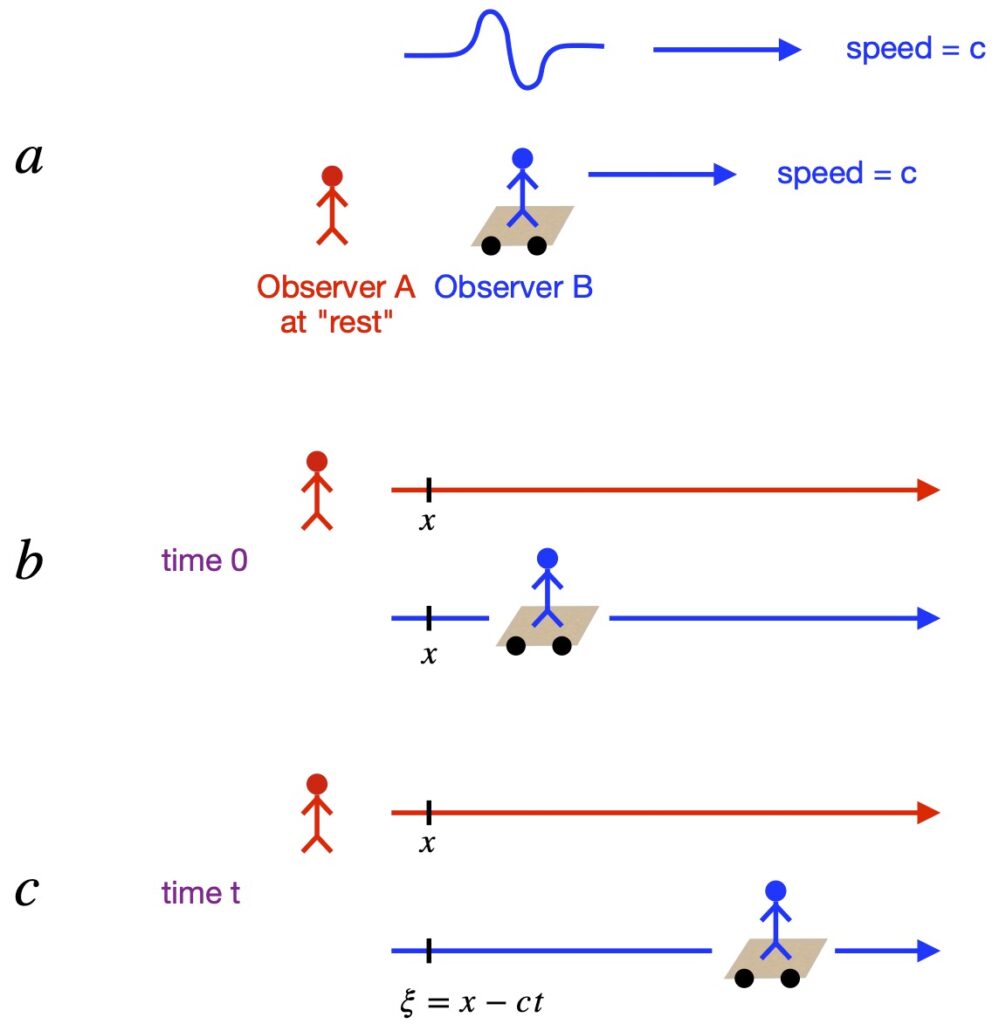
Figure 2.2.1a shows 2 frames of reference: 1) that of Observer A (in red) on the ground and 2) Observer B (in blue) on a cart moving along with a wave, the cart and wave both moving to the right at speed c.
In figure 2.2.1b, taken at time 0, both observers agree on the position of a point, x.
On the other hand, in figure 2.2.1c, taken at time t, Observer A still sees point x at x. However, Observer B has moved ![]() units to the right. Thus, he now sees point x as being at
units to the right. Thus, he now sees point x as being at ![]() .
.
Observer A sees a moving wave. The pde that describes what he sees is the transport equation:
![]()
The question is, What pde describes what Observer B sees?
We know that we’re looking at the same wave so:
![]()
That is, the pde that describes Observer A’s frame of reference, ![]() , equals the pde that describes Observer B’s frame of reference (we’ll call it
, equals the pde that describes Observer B’s frame of reference (we’ll call it ![]() ). We know that
). We know that ![]() is the transport equation. To find
is the transport equation. To find ![]() , we need to translate the terms in the transport equation into the Observer B’s frame of reference. We have:
, we need to translate the terms in the transport equation into the Observer B’s frame of reference. We have:
![]()
and
![]()
We know that:
![]()
![]()
![]()
![]()
![]()
Plugging these values into eq (), we get:
![]()
and
![]()
Now we substitute these values into the transport equation which gives us:
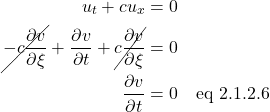
![]() , the derivative of
, the derivative of ![]() with respect to
with respect to ![]() , equaling zero means that
, equaling zero means that ![]() does not change with a change in
does not change with a change in ![]() which means that
which means that ![]() does not depend on
does not depend on ![]() which means that it must be solely a function of
which means that it must be solely a function of ![]() :
:
![]()
Let’s use this to find ![]() . We’ve seen that:
. We’ve seen that:
![]()
But that implies that:
![]()
And that’s the general solution to the transport equation.
II.1.3Wave Equation Solution Using Transport Equation
We want to solve the wave equation:
![]()
Assume that a function, ![]() , solves the wave equation. Let’s see what happens when we plug
, solves the wave equation. Let’s see what happens when we plug ![]() into the transport equation:
into the transport equation:
![]()
I claim that if:
![]()
i.e., if ![]() solves the backward transport equation, the
solves the backward transport equation, the ![]() solves the wave equation. Here’s the proof.
solves the wave equation. Here’s the proof.
Start by substituting the value of ![]() in terms of
in terms of ![]() into eq 2.1.3.2:
into eq 2.1.3.2:
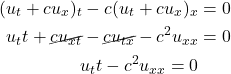
The result of this calculation is, of course, the wave equation. So the only way that equations 2.1.3.1 and 2.1.3.2 can be true is if ![]() solves the wave equation.
solves the wave equation.
Now, if we can find a solution to eq 2.1.3.2 and plug that result into eq 2.1.3.1, then that solution should also be a solution to the wave equation. For example, let ![]() . That means that:
. That means that:
![]()
This is the transport equation. We saw above that the solution to this equation is:
![]()
That implies that ![]() is also a solution to the wave equation.
is also a solution to the wave equation.
We can make the same argument for the reverse transport equation. Let:
![]()
and
![]()
We can show – using arguments similar to those we just used – that if these 2 equations are true, then ![]() is a solution to the wave equation. Then if we take
is a solution to the wave equation. Then if we take ![]() , then:
, then:
![]()
By arguments similar to those used to solve the forward transport equation (except have the cart move to the left rather than right; see section II.1.2) we can solve the backward transport equation. Its solution is:
![]()
Thus, eq 2.1.3.7 is also a solution to the wave equation.
Now the wave equation is a linear equation. Therefore, if ![]() and
and ![]() are both solutions to the wave equation, then
are both solutions to the wave equation, then
![]()
is also a solution to the wave equation. The significance of this formula is that every solution to the wave equation has the form shown in eq 2.1.3.8. We haven’t proved this yet (we’ve just proved that eq 2.1.3.8 is a valid group of solutions to the wave equation). We’ll prove that eq 2.1.3.8 is the general solution to the wave equation next. To do this, I’ll begin with the proof laid out completely in diagrammatic form so the reader can “see the flow” in uninterrupted fashion, then I’ll offer some explanatory text thereafter to fill in the gaps.
Proof:

Here are some explanatory comments for figure 2.3.1.
We’ve shown that the wave equation and the 2 sets of transport equations in blue are equivalent. The solutions to the backward and forward transport equations are given in black. These results can be substituted to get the equations in purple:
![]()
and
![]()
If we add these 2 equations, after some manipulation, we get:
![]()
and
![]()
From the fundamental theorem of calculus, we know that:
![]()
We then integrate eq 2.1.3.11 and eq 2.1.3.12. That gives us, for eq 2.1.3.11:
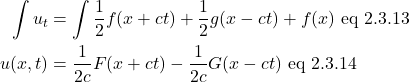
And for eq 2.1.3.12:

Notice that the terms ![]() are the same in eq 2.1.3.13 and eq 2.1.3.15 but extra functions of
are the same in eq 2.1.3.13 and eq 2.1.3.15 but extra functions of ![]() and
and ![]() are seen in these equations, respectively. Eq 2.1.3.13 and eq 2.1.3.15 are equal (because they both equal
are seen in these equations, respectively. Eq 2.1.3.13 and eq 2.1.3.15 are equal (because they both equal ![]() ), but the only way that this can be true is if
), but the only way that this can be true is if ![]() . And the only way that
. And the only way that ![]() can be equal to
can be equal to ![]() is if they are constants. Such constants can be ignored since functions f and g are arbitrary and they could be modified to “absorb” such constants.
is if they are constants. Such constants can be ignored since functions f and g are arbitrary and they could be modified to “absorb” such constants.
Likewise, the constants ![]() and
and ![]() can be absorbed into the arbitrary functions F and G. Thus, the final result is:
can be absorbed into the arbitrary functions F and G. Thus, the final result is:
![]()
And this equation, eq 2.3.17 is the same as eq 2.1.3.8, which is what we were trying to prove.
II.2 d’Alembert’s Formula
A famous formula that gives a large group of solutions to wave equation is d’Alembert’s formula. I won’t go into great detail here but I will give a quick proof.
d’Alembert’s formula is derived from an initial value problem. We have the following conditions:
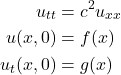
where
![]() is the initial position
is the initial position
![]() is the initial velocity
is the initial velocity
The basic idea is that, if we know the initial position and velocity of a mechanical system, we can predict its state at all future time. Thus, we should be able to determine the state of a wave at all times using this formula.
Recall that the general solution to the wave equation is:
![]()
We’ll find ![]() and
and ![]() by using the initial condition information. We start with:
by using the initial condition information. We start with:
![]()
So
![]()
Next we want to get rid of the derivatives in ![]() and
and ![]() . To do this we integrate eq 2.2.4. When we do the integral, we choose our anitderivative such that
. To do this we integrate eq 2.2.4. When we do the integral, we choose our anitderivative such that ![]() . We have:
. We have:
![]()
Now we solve for ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() :
:
![]()
After some algebra:
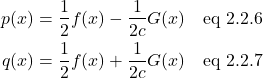
We have an expression for the general solution for the wave equation. We substitute in eq 2.2.6 and 2.2.7. We get:
![Rendered by QuickLaTeX.com \begin{align*} u(x,t) &= \frac12 f(x-ct) - \frac{1}{2c} G(x-ct) + \frac12 f(x+ct) + \frac{1}{2c} G(x+ct) \\ &= \frac12 \left[ f(x+ct) + \frac12 f(x-ct) \right] + \frac{1}{2c} \left[ G(x+ct) - G(x-ct)\right]\\ & \text{eq 2.2.8} \end{align*}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-de25721136693f5b133224a3586a0bcd_l3.png)
But ![]() can be expressed as an integral:
can be expressed as an integral:
![]()
Plugging eq 2.2.9 into eq 2.2.8 yields:
![Rendered by QuickLaTeX.com \begin{align*} u(x,t) &= \frac12 \left[ f(x+ct) + \frac12 f(x-ct) \right] + \frac{1}{2c} \int^{x+ct}_{x-ct} g(s)\,ds \\ & \text{eq 2.2.10} \end{align*}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-11f09fbc647b02c211d1c59912826fbf_l3.png)
Eq 2.2.10 is d’Alembert’s formula.
II.3 Wave Equation Solution: Separation of Variables
We start with the wave equation:
![]()
We assume that the x-terms and t-terms are independent so that the wave equation can be written as:
![]()
Because the x-terms and t-terms are independent, we can pull x-terms out from t-terms like constants and t-terms out from x-terms like constants. We get:
![]()
Next, we “separate the variables” i.e., get all the x-terms on one side and all the t-terms on the other side:
![]()
Now comes the important observation. I’ll quote Fleisch, Dan for this because he states the concept more clearly that I ever could:
The left side depends only on time (t) and does not vary with location (x). The right side depends only on location and does not vary with time. But if this equation is true at every location at every time, then neither side can vary at all (if it did, then, as time passes at a fixed location, the left side would vary but the right side would not [and the sides wouldn’t be equal anymore]). Thus both sides must be constant, and since the sides equal one another, they must equal the same constant.
Fleisch, Dan. “The Wave Equation.” A Student’s Guide to Waves, Cambridge University Press, 2015, p. 71.
Therefore, we can rewrite eq 2.3.4 as follows:
![]()
where ![]() is a constant (referred to as the separation constant).
is a constant (referred to as the separation constant).
Now we need to solve 2 equations:
![]()
and
![]()
To get an idea what potential solutions might look like, we’ll consider 3 cases, depending on the values of the constant terms ![]() or \displaystyle \frac{\lambda}{c^2}:
or \displaystyle \frac{\lambda}{c^2}:
- The constant terms equal 0
- The constant terms are > 0
- The constant terms are < 0
Constants = 0:
![]()
![]()
![]()
![]()
To get solutions to the equation, we recombine ![]() and
and ![]() as:
as:
![]()
Because any linear combination of solutions of this equation is also a solution, and we can make any constant by taking a linear combination with 1, possible solutions that we can combine include: ![]() ,
, ![]() and
and ![]() . So ultimately,
. So ultimately, ![]() is any linear combination of
is any linear combination of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Thus,
. Thus, ![]() is a general solution under this condition.
is a general solution under this condition.
Constants > 0:
To assure that ![]() is positive, we can set it equal to a constant squared. So let
is positive, we can set it equal to a constant squared. So let ![]() . Our equations become:
. Our equations become:
![]()
![]()
![]()
![]()
To see how we arrived at these results, click :
When we recombine these solutions to get solutions to ![]() , we end up with the following base solutions:
, we end up with the following base solutions:
![]()
![]()
![]()
![]()
As before, any linear combination of these base solutions is also a solution. And, of course, functions of the form ![]() can also be expressed as sines and cosines.
can also be expressed as sines and cosines.
Constants < 0
To assure that ![]() is negative, we can set it equal to minus a constant squared. So let
is negative, we can set it equal to minus a constant squared. So let ![]() . Our equations become:
. Our equations become:
![]()
![]()
![]()
![]()
For a quick derivation of these results, click :
These exponential functions can also be expressed as sines and cosines via Euler’s formula:
![]()
![]()
Remember, ![]() . Therefore, we get terms like:
. Therefore, we get terms like:
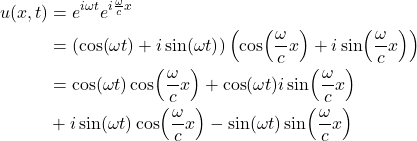
If we were to compute
![]()
![]()
![]()
we would get combinations of ![]() ,
, ![]() ,
, ![]() and
and ![]() , with various signs. Since, ultimately, our solutions will involve any linear combinations of these terms, we can dispense with the
, with various signs. Since, ultimately, our solutions will involve any linear combinations of these terms, we can dispense with the ![]() (because the constant we multiply by can include
(because the constant we multiply by can include ![]() or
or ![]() ). To see this, click .
). To see this, click .
Thus the base functions we can make linear combinations of to get solutions for ![]() are:
are:
![]()
![]()
![]()
![]()
Since
![]()
and
![]()
we can express the above base solutions as:
![]()
and
![]()
These equations are more commonly written as:
![]()
and
![]()
since
![]()
![]()
![]()

![Rendered by QuickLaTeX.com \begin{align*} r^2 e^{rx} - \left(\frac{\omega}{c}\right)^2e^{rx}&=0\\ e^{rx}\left[ r^2 - \left(\frac{\omega}{c}\right)^2 \right]&=0\\ \left( r+\frac{\omega}{c} \right)\left( r-\frac{\omega}{c} \right)&=0\\ r=-\frac{\omega}{c} \quad r=\frac{\omega}{c} & \end{align*}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-4d0a7cf1390d7d4ea573a04c9f0ce987_l3.png)