Green’s Function

Motivation

Green’s function is a method for solving differential equations, the classic example being second order linear non-homogeneous differential equations of the form:

D_x f(x) = g(x) \quad \text{(1)}  where

D_x is an operator (e.g., the Laplacian, \displaystyle \frac{d^2}{dx^2})
f(x) is what we’re solving for
g(x) is the resultant function

Drawing an analogy with matrix equations may be helpful to understand the general strategy underlying use of Green’s function. In matrix equations, we multiply both sides of the equation by the inverse of the matrix (i.e., operator) that takes in the vector we want to find and spits out the resultant vector:

D\ket{f}=\ket{g}

So,

D^1D\ket{f} = D^{-1}\ket{g} + \displaystyle \sum_i c_i \ket{h_i}

and

\ket{f} = D^{-1}\ket{g} + \displaystyle \sum_i c_i \ket{h_i} \quad \text{where} \, D\ket{h_i}=0 \quad \text{(2)}

Similarly:

D_xG(x,x^{\prime})g(x^{\prime})f(x) = \displaystyle \int dx^{\prime}\, [D_xG(x,x^{\prime})]\, g(x^{\prime}) + \displaystyle \sum_i c_i h_i(x)
                =\displaystyle \int dx^{\prime} \,[I]\, g(x^{\prime}) + \displaystyle \sum_i c_i h_i(x)
                =\displaystyle \int dx^{\prime} g(x^{\prime}) + \displaystyle \sum_i c_i h_i(x)

which (removing D_x) implies:

f(x) = \displaystyle \int dx^{\prime} G(x,x^{\prime})g(x^{\prime}) + \displaystyle \sum_i c_i h_i(x) \quad \text{(3)}

Where G(x,x^{\prime}) is the analogue of D^{-1} in eq. (2). Specifically:

G(x,x^{\prime}) = \bra{x}D^{-1}\ket{x^{\prime}}

We get this by multiplying both sides of eq. (2) by \bra{x}:

\bra{x}\ket{f} = f(x) = \bra{x}D^{-1} (\sum dx^{\prime} \ket{x^{\prime}})\bra{x^{\prime}}\ket{g} + \sum_i c_i \bra{x}\ket{h_i} \quad \text{(4)}

Also in eq. (4), \bra{x^{\prime}}\ket{g} is analogous to g(x) and \bra{x}\ket{h_i} is analogous to h(x).

In this analogy, G(x,x^{\prime}) is the Green’s function.

And just as:

DD^1 = \bra{x}\ket{x^{\prime}} = I where I is the identity matrix

D_x G(x,x^{\prime}) = \delta(x-x^{\prime}) \quad \text{(5)}

So we find the Green’s function, put it back into eq. (3) and that should give us f(x).

Finding Green’s Function

To find Green’s function, we need to impose some boundary conditions to find the constants that are associated with its solution. We’ll illustrate the concepts via a classic case – finding the Green’s function for the Laplacian operator \displaystyle \frac{d^2}{dx^2}. We start with:

\displaystyle \frac{d^2\,f(x)}{dx^2}=g(x) \quad \text{(6)}

Let’s establish some boundary conditions for this equation:

x \in [0,\pi] \quad \text{with} \quad f(0) = f(\pi) = 0

Furthermore, by definition:

\displaystyle \frac{d^2 G(x,x^{\prime})}{dx^2}=\delta(x-x^{\prime}) \quad \text{(7)}

We need to solve this equation for 2 cases:

Case 1: 0 \leq x < x^{\prime}

Since x^{\prime} isn’t within the boundary condition, \delta(x-x^{\prime})=0 so:

\displaystyle \frac{d^2 G(x,x^{\prime})}{dx^2}=0\quad \text{(8)}

Therefore:

G_L(x,x^{\prime})=A x + B
G_L(0,x^{\prime})=A \cdot 0 + B=0 \,\,\Rightarrow\,\, B = 0
G_L(x,x^{\prime})=Ax \quad \text{(9)}

Case 2: x^{\prime} < x \leq 1

Since x^{\prime} isn’t within the boundary condition, \delta(x-x^{\prime})=0 so:

\displaystyle \frac{d^2 G(x,x^{\prime})}{dx^2}=0

G_R(x,x^{\prime})=C x + D
G_R(1,x^{\prime})=C \cdot \pi + D=0\,\,\Rightarrow\,\, D=-C\pi
G_R(x,x^{\prime})=C(x-\pi) \quad \text{(10)}

We have 2 other pieces of information:

Condition A: At x=x^{\prime}, G_L(x,x^{\prime})=G_R(x,x^{\prime}) which means:

A x^{\prime} = C(x^{\prime} - \pi) \quad \text{(11)}

Condition B: Recall that \displaystyle \frac{d^2 G(x,x^{\prime})}{dx^2}=\delta(x-x^{\prime}). Therefore,

\displaystyle \int_{x^{\prime}-\epsilon}^{x^{\prime}+\epsilon} \displaystyle \frac{d^2 G(x,x^{\prime})}{dx^2} = \eval{\frac{dG}{dx}}_{x^{\prime}-\epsilon}^{x^{\prime}+\epsilon} = \delta(x-x^{\prime})\quad \text{(12)}

\displaystyle \lim_{\epsilon \rightarrow 0^+} \frac{\partial G}{\partial x}} - \displaystyle \lim_{\epsilon \rightarrow 0^-} \frac{\partial G}{\partial x}} = 1\quad \text{(13)}

\displaystyle \frac{\partial G_L}{\partial x} - \displaystyle \frac{\partial G_R}{\partial x} = 1\quad \text{(14)}

We saw before:

G_L(x,x^{\prime})=Ax \quad \text{(9)}

and

G_R(x,x^{\prime})=Cx - C\pi \quad \text{(10)}

Thus:

\displaystyle \frac{\partial G_L}{\partial x} = A \quad \text{(11)}

and

\displaystyle \frac{\partial G_R}{\partial x} = C \quad \text{(12)}

Then:

\displaystyle \frac{\partial G_L}{\partial x} - \displaystyle \frac{\partial G_R}{\partial x} = 1 \quad \text{(13)}

which implies:

C - A = 1
C = 1 + A \quad \text{(14)}

Substituting this result into eq. (11), we get:

    \begin{align*} \cancel{A x^{\prime}} &= C(x^{\prime}-\pi)\\ &= (1+A)(x^{\prime}-\pi)\\ &= x^{\prime} - \pi + \cancel{A x^{\prime}} -A\pi\\ 0 &= x^{\prime} - \pi - A\pi \\ A\pi &= x^{\prime} - \pi \\ A &= \displaystyle \frac{x^{\prime} - \pi}{\pi} \\ & \\ C &= 1 + A \\ &= \displaystyle \frac{\pi}{\pi} + \displaystyle \frac{x^{\prime} - \pi}{\pi} \\ &= \displaystyle \frac{x^{\prime}}{\pi} \end{align*}

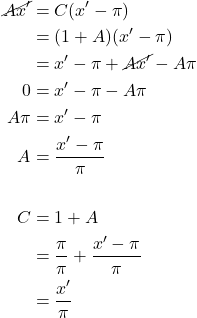
Putting this all together, we have:

G(x,x^{\prime})= \begin{cases} \displaystyle \frac{x^{\prime} - \pi}{\pi}x, & 0 \leq x < x^{\prime} \\ \displaystyle \frac{x^{\prime}}{\pi}(x-\pi), & x^{\prime} < x \leq \pi \end{cases}

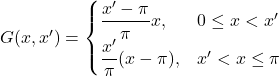
Examples

One of the most important Green’s function is that for Poisson’s equation. I derive that Green’s function for – and find the particular solution to – this equation at the following link:

Poisson’s Equation