Right-angled triangle definitions
In this way of looking at things, basic trigonometric functions are defined as ratios of the lengths of the sides of a right triangle.
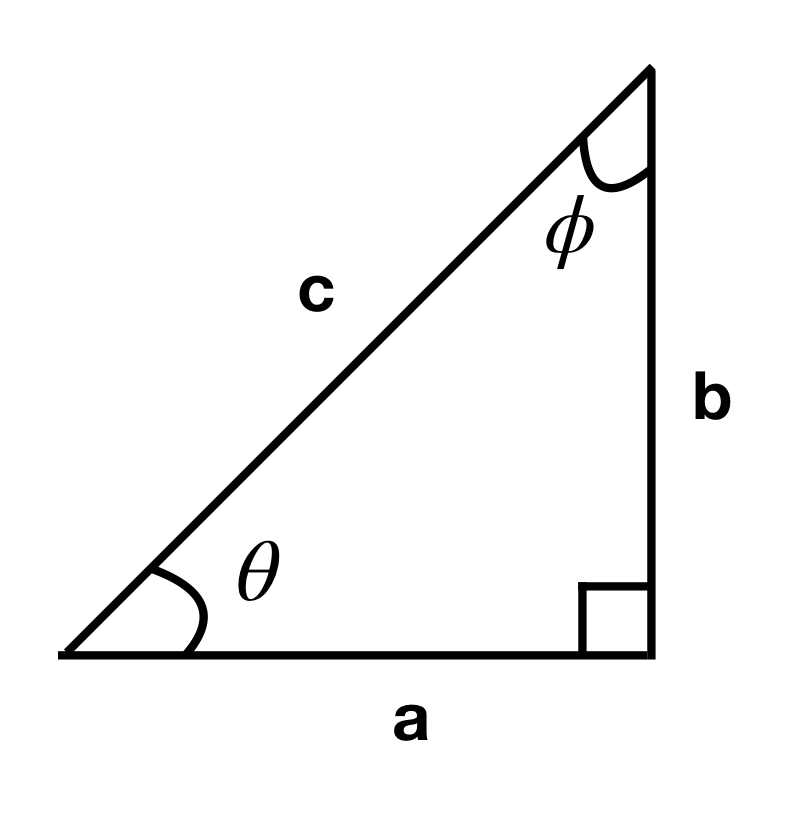
Figure 1 shows a right triangle i.e., a triangle where one of its angles = 90º. Such an angle is referred to as a right angle, thus the name. The triangle above consists of 2 sides, a and b, that join to form the right angle. The little box nestled in the angle formed by sides a and b indicates that angle is a right angle. The side opposite the right angle, c, is called the hypotenuse of the triangle. Sides a and c form the angle ![]() . Sides b and c form angle
. Sides b and c form angle ![]() . Side a is said to be adjacent to
. Side a is said to be adjacent to ![]() . Side b is said to be adjacent to
. Side b is said to be adjacent to ![]() .
.
Given this setup, the following functions can be defined for ![]() :
:
Sine (= sin)
(1) ![]()
Cosine (= cos)
(2) ![]()
Tangent (= tan)
(3) ![]()
Cotangent (= cot)
(4) ![]()
Secant (= sec)
(5) ![]()
Cosecant (= csc)
(6) ![]()
Unit-circle definitions
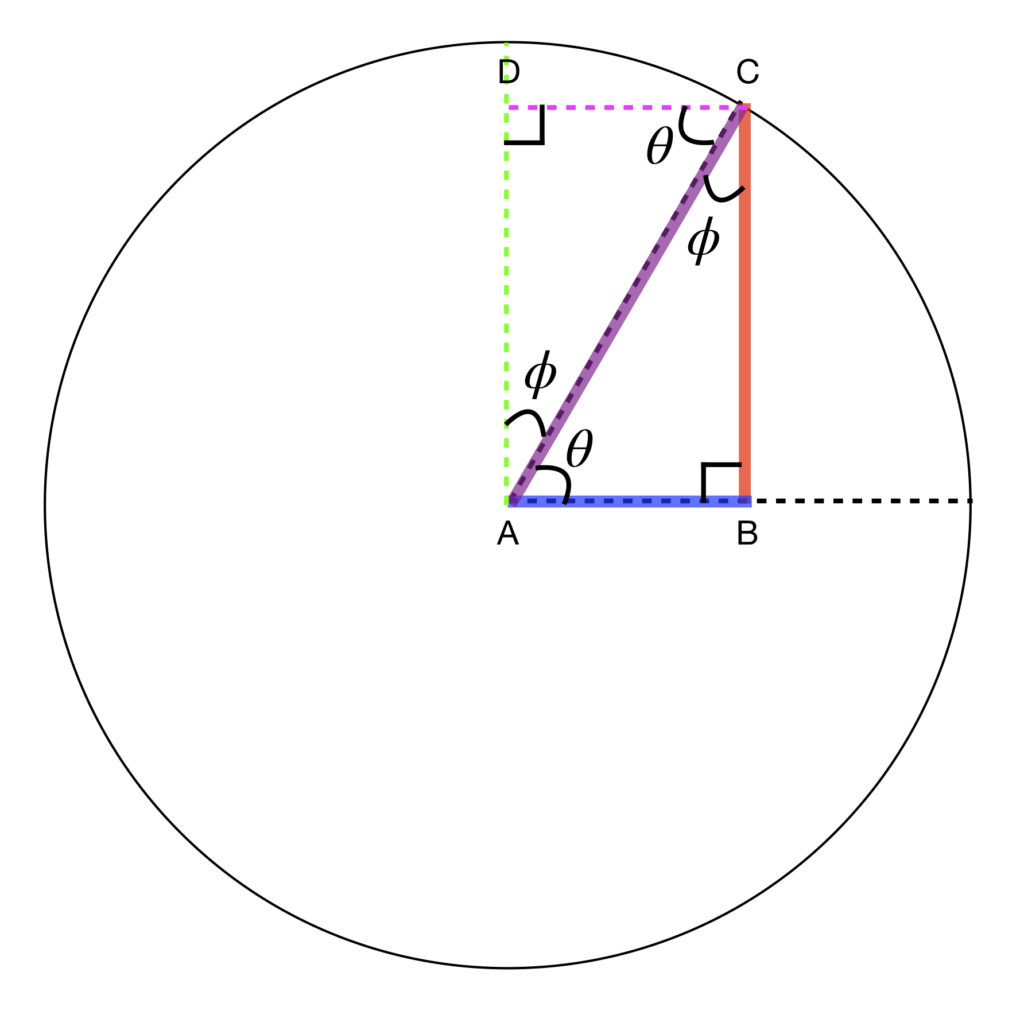
In this way of looking at things, the trigonometric functions are defined as coordinate values of points in the Euclidean plane that are related to a unit circle. A unit circle, in turn, is a circle with its center at the origin of a Euclidean coordinate system and a radius of length equal 1 unit. The radius of a circle, of course, is the length of a line segment connecting the center of the circle and any point on the circle. In figure 2, AC is a radius. It is also the hypotenuse of triangle ABC.
Also,
- The x-coordinate of point C is
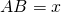
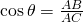
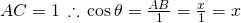 , the x-coordinate of C
, the x-coordinate of C
- The y-coordinate of point C is BC.
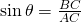
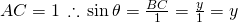 , the y-coordinate of C
, the y-coordinate of C
- Since
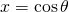 and
and 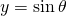 , the coordinates of the point C are
, the coordinates of the point C are 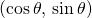
An excellent summary of this topic can be found at Khan Academy.
Graphs of Trigonometric Function
Graphs of the basic trigonometric functions can be found at SparkNotes.
