Statement:
![]()
Proof:
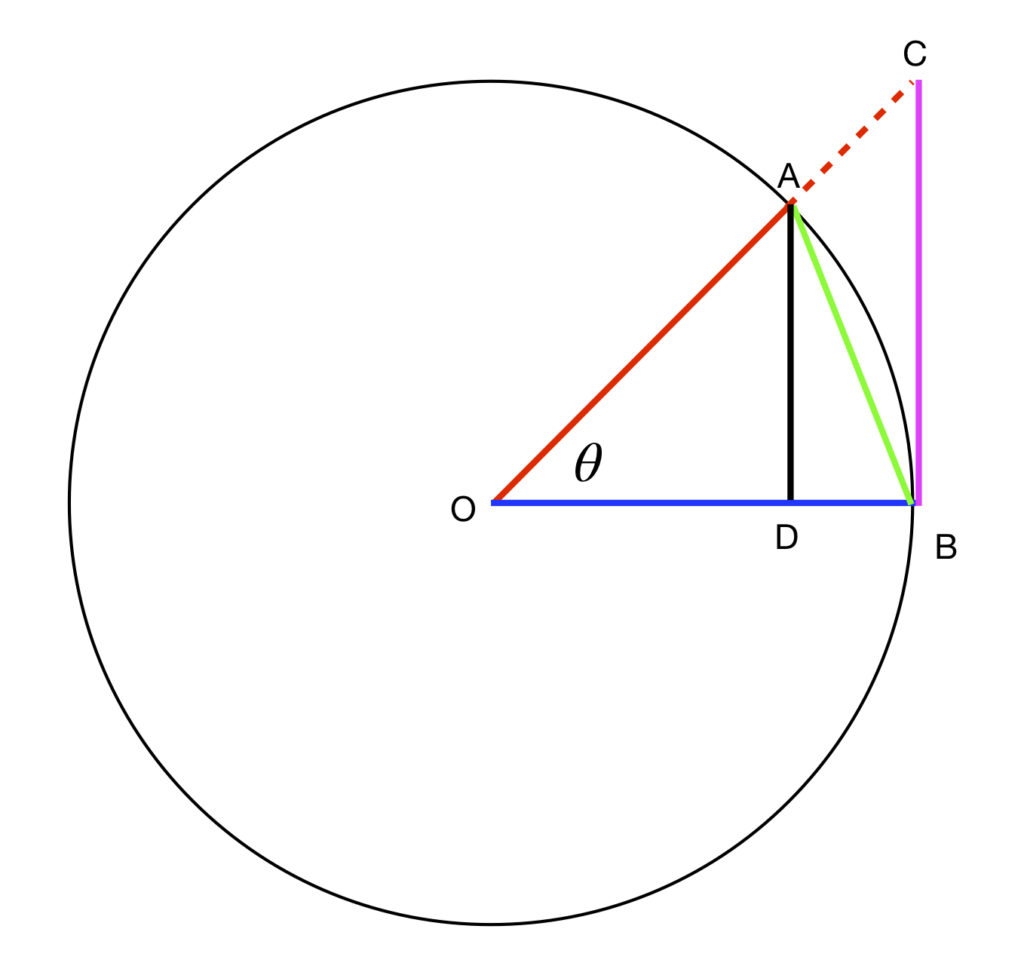
The circle in figure 1 is a unit circle. ![]() and
and ![]() are radii. Therefore,
are radii. Therefore,
![]()
![]()
![]()
We need to calculate the area of the arc between ![]() and
and ![]() swept out over
swept out over ![]() . this calculation goes as follows:
. this calculation goes as follows:
- The circumference of the entire circle is given by
 .
. - The length of the arc between
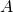 and
and 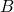 is
is  (where
(where 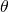 is expressed in radians)
is expressed in radians) - The fraction of the circle made up from the arc between
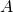 and
and 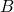 , therefore, is given by
, therefore, is given by 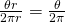
- The area of the entire circle is equal to
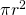
- The fraction of the area of the circle made from the arc between
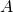 and
and 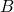 , then, equals
, then, equals 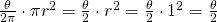 so,
so, 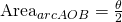
Next, we need to calculate the areas of ![]() and
and ![]() .
.
![]() :
:
- The area of a triangle is
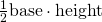 .
. - The base is the radius of the circle, 1.
- The height is
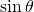 .
. - Therefore,
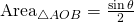
![]() :
:
- The area of a triangle is
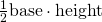 .
. - The base is the radius of the circle, 1.
- The height is
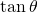 . Why? Because
. Why? Because 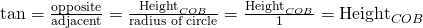 .
. - Therefore,
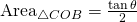
Just by looking at the diagram, we can see that:
![]()
Thus,
![]()
Multiply through by 2:
![]()
Divide through by ![]() :
:
![]()
Take the reciprocal of this equation:
![]()
Notice that we changed the ![]() sign to
sign to ![]() . Why? Here’s an example:
. Why? Here’s an example:
![]()
The squeeze theorem states that:
- If
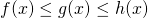 and
and - If
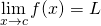 and
and 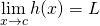
- Then
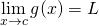
To apply the squeeze theorem to our problem, let
And take the limit as ![]() of the equation
of the equation ![]() . We get:
. We get:

Therefore,
![]()
