![]()
From the basic trigonometry identity for the sine of two added angles:
![]() therefore,
therefore,
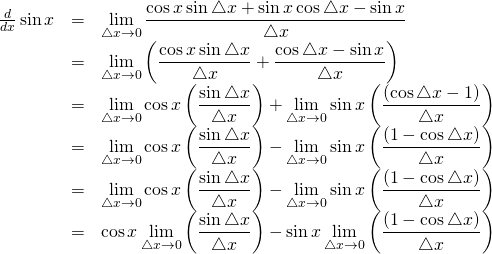
However,
![]() (see proof)
(see proof)
and
![]() (see proof)
(see proof)
Therefore,
![]()
That means that
![]()
Musings on science, religion, etc.
![]()
From the basic trigonometry identity for the sine of two added angles:
![]() therefore,
therefore,
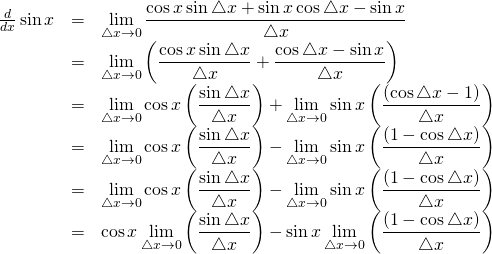
However,
![]() (see proof)
(see proof)
and
![]() (see proof)
(see proof)
Therefore,
![]()
That means that
![]()