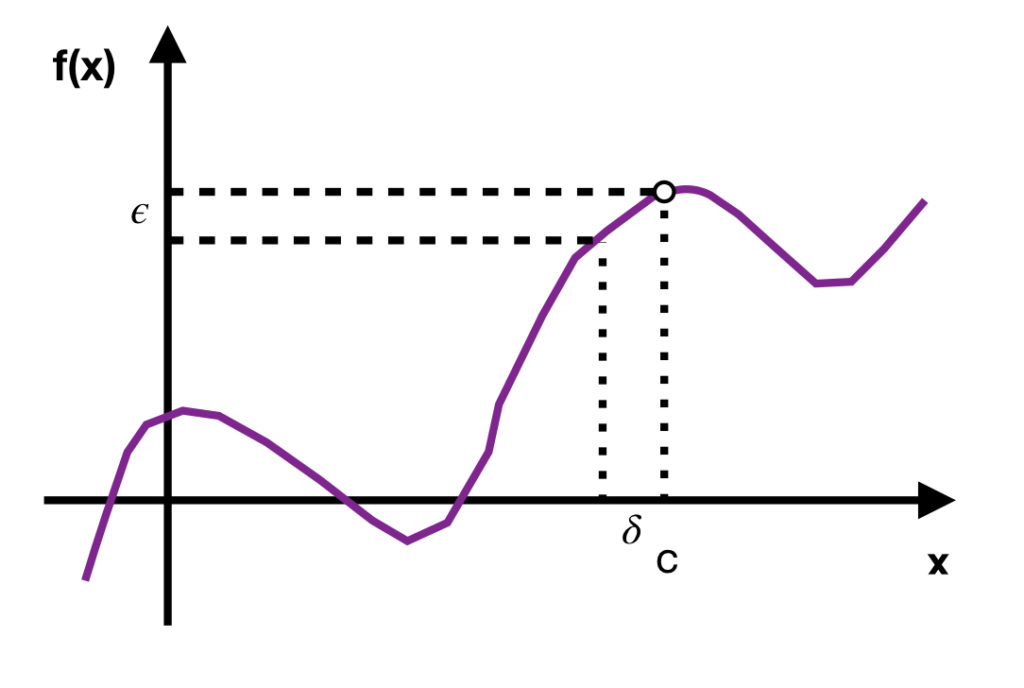
The limit ![]() exists if
exists if
- if, for any
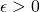 and
and 
- there exist
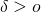 such that
such that 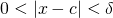
Stated in words, no matter how close ![]() gets to some value
gets to some value ![]() , you can always find a value of
, you can always find a value of ![]() that’s very close to
that’s very close to ![]() .
.
Said another way, as ![]() gets closer and closer to some number
gets closer and closer to some number ![]() (without actually getting to
(without actually getting to ![]() ),
), ![]() gets closer and closer to some value (without actually reaching that value). That value,
gets closer and closer to some value (without actually reaching that value). That value, ![]() that
that ![]() is approaching is called the limit of
is approaching is called the limit of ![]() as
as ![]() approaches
approaches ![]() .
.
Notice the phrases “without actually getting to” and “without actually reaching”. This implies that a function can have a limit without that limit actually being a value of a function. To illustrate this, in the diagram, ![]() is purposely shown to be discontinuous at
is purposely shown to be discontinuous at ![]() , yet
, yet ![]() still exists (i.e., its value is
still exists (i.e., its value is ![]() ).
).
