Sum of zeros of a polynomial – Sam Artigliere's Blog

Consider the polynomial equation

$x^n+a_1x^{n-1}+\dots+a_{n-1}x+c=0$

where $x$ is a variable and the $a\text{'}$ s, $n$ and $c$ are constants.

We know that we can factor this polynomial into so-called “zeros” (i.e., terms that, when set to zero and solved, yield values for $x$ that are roots of – that is, answers to – the equation):

$(x-r_1)(x-r_2)\cdots(x-r_n)=0\quad \Rightarrow$

$x_1=r_1$ , $x_2=r_2$ , $\dots$ $x_n=r_n$ .

Here, the $r\text{'}$ s are the roots.

What we want to prove is that the coefficient, $a_1$ , for the $x^{n-1}$ term in the polynomial equation is equal to the sum of the roots:

$a_1=r_1+r_2+\dots+r_n$

The proof we will use is a proof by induction taken from Khan Academy:

https://www.khanacademy.org/math/math-for-fun-and-glory/aime/2003-aime/v/sum-of-polynomial-roots-proof

Let’s assume that what we want to prove is true, that a polynomial

$x^n+a_1x^{n-1}+\text{(other stuff we don't care about)}$

Has roots

$r_1,r_2,\cdots,r_n$

and that

$a_1=r_1+r_2+\dots+r_n$

That’s the same as saying that the product of the “zeros” can be multiplied out as follows:

$(x-r_1)(x-r_2)\cdots(x-r_n)=0 \quad \rightarrow \quad x^n+(r_1+r_2+\dots+r_n)x^{n-1}+\,\dots=0$

Now consider the polynomial

$x^{n+1}+a_1x^n+\dots$

It’s roots are

$r_1,r_2,\cdots,r_n,r_{n+1}$

And

$a_1=r_1+r_2+\dots+r_n+r_{n+1}$

The product of “zeros” that goes along with this polynomial is

$(x-r_1)(x-r_2)\cdots(x-r_n)(x-r_{n+1})=0$

This can be extended by multiplying the expression of the product of zeros we had before by an additional “zero”, $x-r_{n+1}$ :

$\underbrace{(x-r_1)(x-r_2)\cdots(x-r_n)}_{\text{prior}} \underbrace{(x-r_{n+1})}_{\text{new}}=0$

Next, we multiplied out the expression on the left side of this equation:

$\left[ x-r_{n+1} \right]\left[x^n-(r_1+r_2+\dots+r_n)x^{n-1}+\,\dots\right]=0$

That gives us:

$\begin{array}{rcl}x\cdot x^n - x\cdot(r_1+r_2+\dots+r_n)x^{n-1}-r_{n+1}\cdot x^n + \,\dots &=& 0 \\ x^{n+1}-(r_1+r_2+\dots+r_n)x^n - r_{n+1}\cdot x^n + \,\dots &=& 0 \\ x^{n+1}-(r_1+r_2+\dots+r_n+r_{n+1})x^n + \,\dots &=& 0 \end{array}$

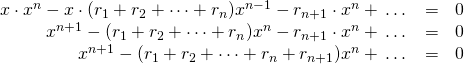
So if the sum of the roots equals minus the coefficient for the $x^{n-1}$ term of a polynomial in the case where the highest degree term is $n$ as well as in the case where the highest degree term is $n+1$ , it will be true for any degree polynomial.

Here are two examples:

Example 1:

$x^2+a_1x+a_2$

This equation can be written as $(x-r_1)(x-r_2)=0\quad \text{where}$

$(x-r_1)$ and $(x-r_2)$ are the “zeros”

and

$r_1$ and $r_1$ are the roots.

If we expand the above equation, we get:

$x^2-r_1x-r_2x+r_1r_2=x^2-(r_1+r_2)x+r_1r_2=0$

But coefficient of the $x^{n-1}$ term ( $x$ in this case) is $r_1+r_2$ which, of course, is the sum of the roots, just as our theorem predicts.

Example 2

Now let’s consider a slightly more complex case, the case where $n=3$ :

$x^3+a_1x^2+a_2x+a_3$

Again, our concern will be $a_1$ , the coefficient of the $x^{n-1}$ term, which in this case, is $x^2$ . We know that when the above equation is factored, we end up with the product of three “zeros” equal to zero:

$(x-r_1)(x-r_2)(x-r_3)=0$ where $r_1$ , $r_2$ and $r_3$ are the roots of the solution.

We multiply out the “zeros” equation to get a polynomial. Since $(x-r_1)(x-r_2)=x^2-(r_1+r_2)x+r_1r_2$ , the easiest way to do this is to multiply the latter equation by $(x-r_3)$ . Start with the $x$ term:

$x\left[ x^2-(r_1+r_2)x+r_1r_2 \right]=x^3-(r_1+r_2)x^2 + \dots$

Now we’ll multiply by the $-r_3$ term:

$-r_3\left[ x^2-(r_1+r_2)x+r_1r_2 \right]=-r_3 x^2+\dots$

Add the results of the right side of the last two equations together. We get:

$x^3-(r_1+r_2)x^2-r_3 x^2+\dots=x^3-(r_1+r_2+r_3)x^2+\dots$

But the coefficient of the $x^2$ term, $(r_1+r_2+r_3)$ , is the sum of the roots, which is what we hoped to show.