Contents
Introduction
Joseph Fourier (3/21/1768 – 5/16/1830) realized that any function can be estimated as a sum sines and cosines, now known as Fourier’s theorem. This led to development of the mathematical functions known as the Fourier transformation and inverse Fourier transformation, functions that have widespread applications throughout mathematics and science. The goal of this article is to perform an as-simple-as-possible explanation of this theorem and these functions.
Fourier’s theorem
Suppose we have a function of time, ![]() , where
, where ![]() . A graph of this functions and the 2 individual functions that add together to create it are shown in the diagram below:
. A graph of this functions and the 2 individual functions that add together to create it are shown in the diagram below:
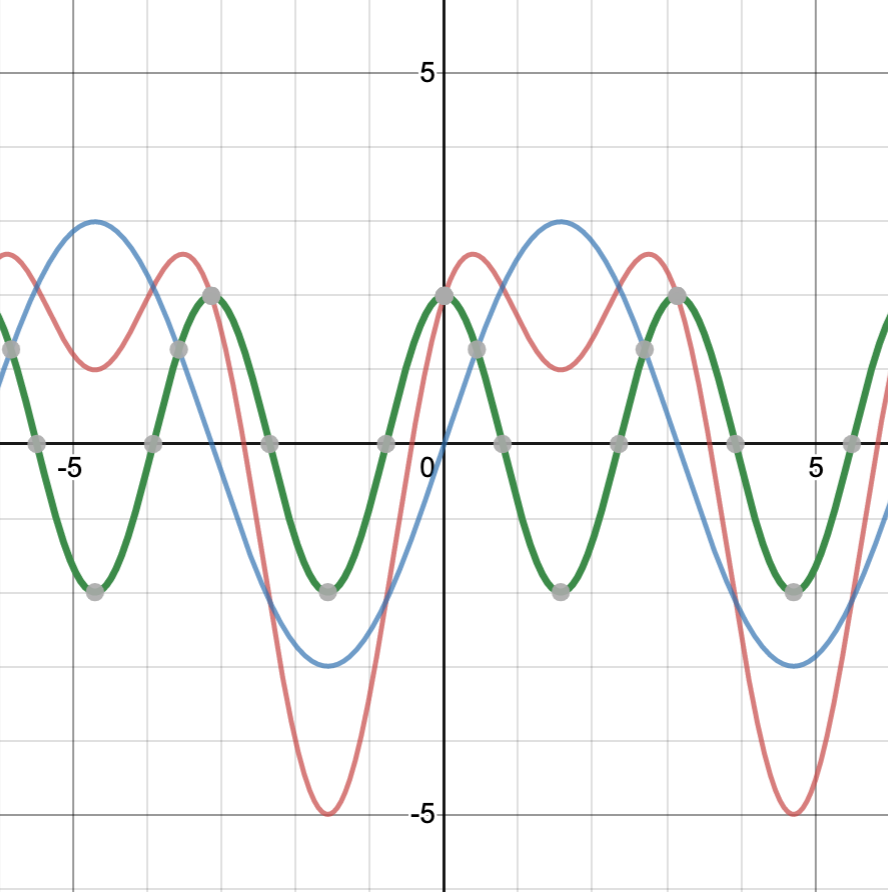
Blue –
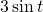
Green –
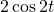
Red –
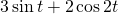
In figure 1, ![]() is represented on the axis (horizontal axis) and
is represented on the axis (horizontal axis) and ![]() is represented on the abscissa (vertical axis). Let’s consider the values of
is represented on the abscissa (vertical axis). Let’s consider the values of ![]() for the 3 functions at 3 points:
for the 3 functions at 3 points: ![]() ,
, ![]() and
and ![]() :
:
For ![]() ,
,
For ![]() ,
,
For ![]() ,
,
For the 3 points we considered, we can see that if we add the values of sine and cosine functions at those points, we get the value of a new periodic function (i.e., a function that repeats itself periodically, or more formally, one where ![]() ,
, ![]() being the length of
being the length of ![]() the function spans before it repeats itself). It turns out that, if we add the values of the functions depicted by the blue and green lines at every point, we get the value of the function represented by the red curve. The conclusion we can draw from this example is that, by adding simple sine and cosine functions with varying amplitudes and frequencies, we can create a more complex periodic function. It shouldn’t be too much of a stretch, then, to think that if we add up enough sines and cosines with the appropriate combination of amplitudes and frequencies, then we can approximate any periodic function we want to very closely. Furthermore, if we could add an infinite number of sines and cosines together with just the right amplitudes and frequencies, we could specify any periodic function exactly. And finally, if we consider the period of a complex function to be infinite (i.e., the function goes on forever without repeating itself) then any function can be represented by a weighted sum of cosines and sines. These are the ideas on which Fourier theory is based.
the function spans before it repeats itself). It turns out that, if we add the values of the functions depicted by the blue and green lines at every point, we get the value of the function represented by the red curve. The conclusion we can draw from this example is that, by adding simple sine and cosine functions with varying amplitudes and frequencies, we can create a more complex periodic function. It shouldn’t be too much of a stretch, then, to think that if we add up enough sines and cosines with the appropriate combination of amplitudes and frequencies, then we can approximate any periodic function we want to very closely. Furthermore, if we could add an infinite number of sines and cosines together with just the right amplitudes and frequencies, we could specify any periodic function exactly. And finally, if we consider the period of a complex function to be infinite (i.e., the function goes on forever without repeating itself) then any function can be represented by a weighted sum of cosines and sines. These are the ideas on which Fourier theory is based.
Fourier series
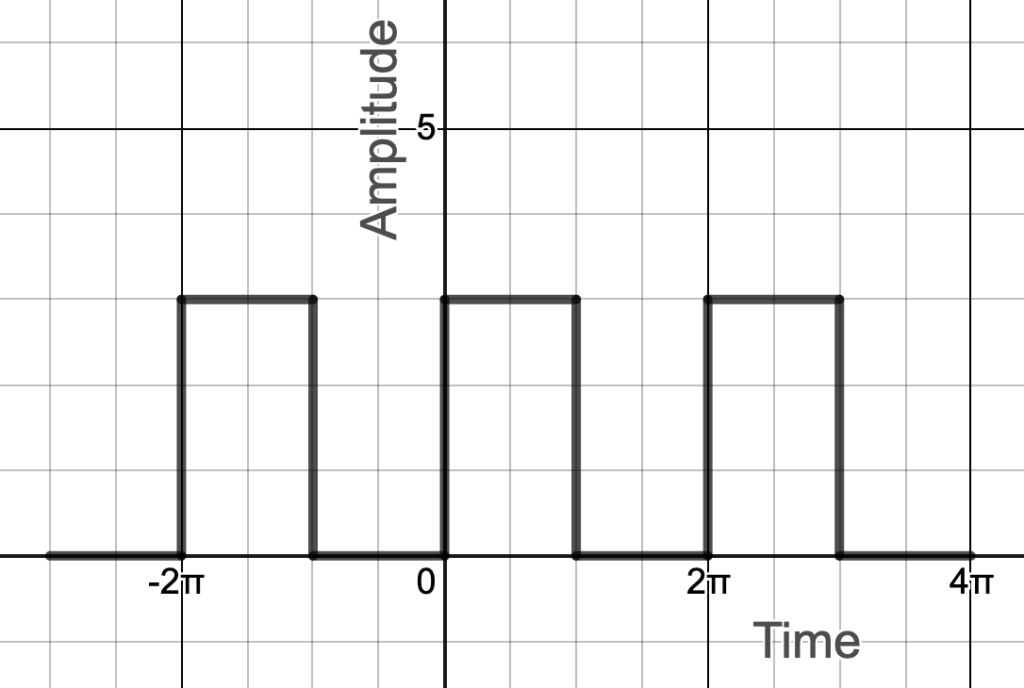
Square function
To elucidate this theory, let’s start by deriving the so-called Fourier series for a simple periodic function – the square wave. This derivation is taken from Khan Academy. It begins at the following link:
Fourier series derivation
The square function shown in figure 2 repeats itself over a period of ![]() so we should be able to use a sum of cosines and sines to make an approximation. Such an approximation is expressed mathematically as
so we should be able to use a sum of cosines and sines to make an approximation. Such an approximation is expressed mathematically as
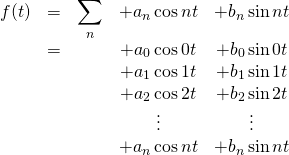
Because
many authors separate the ![]() and
and ![]() terms, replacing them with
terms, replacing them with ![]() . If we do this, our equation becomes
. If we do this, our equation becomes
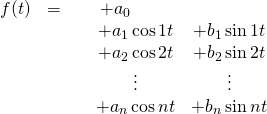
Fourier coefficient derivation
What we’d like to do is find the coefficients ![]() and
and ![]() . Before we do, let’s take a moment and consider the meaning of these coefficients. The best way to visualize this is to consider
. Before we do, let’s take a moment and consider the meaning of these coefficients. The best way to visualize this is to consider ![]() a signal in the time domain. That is, it’s a plot of the amplitude of a complex wave made up of a bunch of sine and cosine waves of differing frequencies and different amplitudes, versus time. The coefficients,
a signal in the time domain. That is, it’s a plot of the amplitude of a complex wave made up of a bunch of sine and cosine waves of differing frequencies and different amplitudes, versus time. The coefficients, ![]() and
and ![]() , are the amplitudes for each given frequency. They tell us, how much each frequency contributes to the time-domain signal.
, are the amplitudes for each given frequency. They tell us, how much each frequency contributes to the time-domain signal.
Now on to the derivation of expressions for the coefficient values. For this derivation, we need the following information:
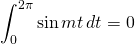 for all integers
for all integers 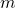
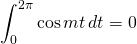 for all nonzero integers
for all nonzero integers 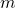
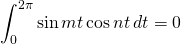 for all integers
for all integers 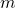 and
and 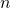
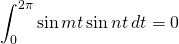 for all integers
for all integers 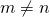 or
or 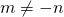
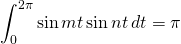 for nonzero integers
for nonzero integers 
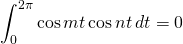 for all integers
for all integers 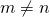 or
or 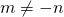
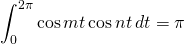 for nonzero integers
for nonzero integers 
Proof of the above equations can be found here.
Let’s start with ![]() . Consider the equation:
. Consider the equation:
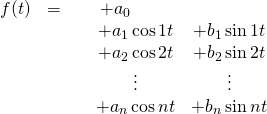
Take the integral from ![]() to
to ![]() of both sides of the equation:
of both sides of the equation:
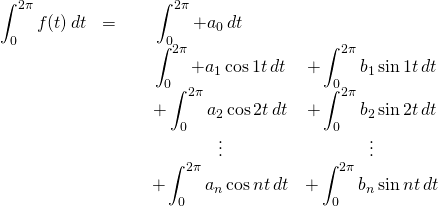
We’ve already established that
Therefore, all of the terms on the righthand aspect of the equation above disappear except the ![]() term. We have:
term. We have:
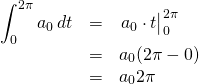
which means that
![]()
But ![]() is the area under the curve
is the area under the curve ![]() from
from ![]() to
to ![]() and
and ![]() is the value of the “base” of the complex shape we’re taking the area under. Thus, dividing
is the value of the “base” of the complex shape we’re taking the area under. Thus, dividing ![]() by
by ![]() is just the average value of the function
is just the average value of the function ![]() .
.
Next, lets calculate an expression for the coefficients ![]() . We begin again with our expression for
. We begin again with our expression for ![]() , multiply both sides by
, multiply both sides by ![]() then take
then take ![]() of both sides. We get
of both sides. We get
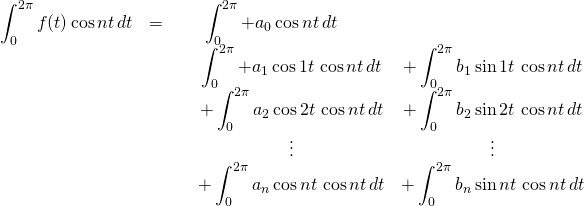
We know that
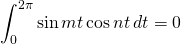
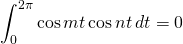 for all integers
for all integers 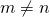 or
or 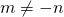
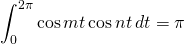 for nonzero integers
for nonzero integers 
Thus, all of the terms on the righthand side of the equation above evaluate to 0 except
![]()
So,
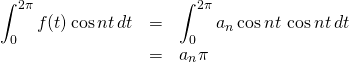
Therefore,
![]()
You might be wondering why the integral ![]() doesn’t evaluate to 0 since we’ve been saying that
doesn’t evaluate to 0 since we’ve been saying that ![]() . If so, click .
. If so, click .
Let’s move on now to calculation of the coefficients ![]() . The derivation is similar to that for
. The derivation is similar to that for ![]() . Again, we start with the expression for
. Again, we start with the expression for ![]() . But his time we multiply all terms by
. But his time we multiply all terms by ![]() and take the integral
and take the integral ![]() of each term. This gives us
of each term. This gives us
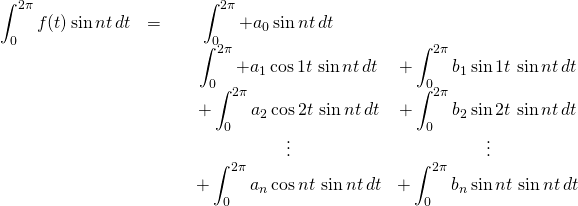
We know that
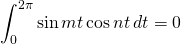
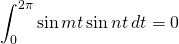 for all integers
for all integers  or
or 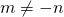
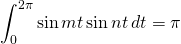 for nonzero integers
for nonzero integers 
Thus, all of the terms on the righthand side of the equation above evaluate to 0 except
![]()
So,
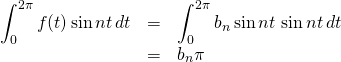
Therefore,
![]()
In summary,
Fourier series of square function
We’ll now use the formulas for the Fourier coefficients we just derived to calculate the Fourier series of the square function pictured in figure 2.

We’ll start by calculating ![]() . From the diagram, note that the value of
. From the diagram, note that the value of ![]() from
from ![]() to
to ![]() is 3 and from
is 3 and from ![]() to
to ![]() , it’s 0. Therefore,
, it’s 0. Therefore,
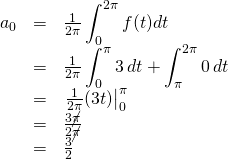
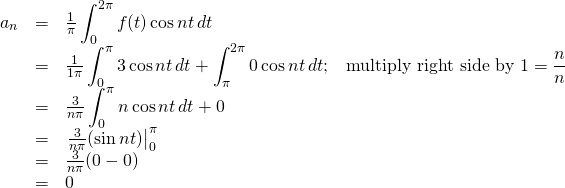
![Rendered by QuickLaTeX.com \begin{array}{rcl} a_n&=&\frac{1}{\pi}\displaystyle\int_0^{2\pi}f(t)\sin nt\,dt\\ &=&\frac{1}{1\pi}\displaystyle\int_0^{\pi}3\sin nt\,dt + \displaystyle\int_\pi^{2\pi}0\cos nt\,dt\text{;}\quad \text{multiply right side by }1= \frac{-n}{-n}\\ &=&\frac{3}{-n\pi}\displaystyle\int_0^{\pi}-n\sin nt\,dt + 0\\ &=&\eval{\frac{-3}{n\pi}(\cos nt)}_0^\pi\\ &=&\frac{-3}{n\pi}[(\cos n\pi)-(\cos n\cdot 0)] \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-a0cbe887a86867b1495536c3dda9d802_l3.png)
If ![]() is even, then
is even, then
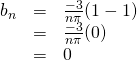
If ![]() is odd, then
is odd, then
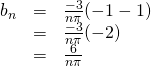
Putting everything together, the Fourier series for a square wave is:
![]()
Notice that the Fourier series above contains only sine terms. This is because it is an odd function. Let me explain.
Functions can be classified as even, odd or neither even nor odd. Even functions are functions that are symmetric around the y-axis (in Cartesian coordinates). That is, ![]() .
. ![]() and
and ![]() are examples of even functions. On the other hand, odd functions are functions that are symmetric about the origin (in Cartesian coordinates). That is,
are examples of even functions. On the other hand, odd functions are functions that are symmetric about the origin (in Cartesian coordinates). That is, ![]() .
. ![]() and
and ![]() are examples of odd functions. Even functions can be approximated by a sum of cosines. Odd functions can be approximated by as sum of sines. A proof of this can be found at the following link (although information presented later in this article is needed to understand this proof):
are examples of odd functions. Even functions can be approximated by a sum of cosines. Odd functions can be approximated by as sum of sines. A proof of this can be found at the following link (although information presented later in this article is needed to understand this proof):
http://mathonline.wikidot.com/trigonometric-fourier-series-of-even-and-odd-functions
Most functions, however, fall into the “neither” category. To represent these, a sum of both cosines and sines are needed. This is why the expression for the Fourier series we started with contains both cosine and sine terms.
Complex Fourier series
Series derivation
We can express the Fourier series in a more complex form using exponential functions. Specifically, from Euler’s formula, we have
![]()
It will be most useful to us if we multiply the righthand part of the righthand equation by ![]() :
:
![]()
We plug these into our expression for the Fourier series:
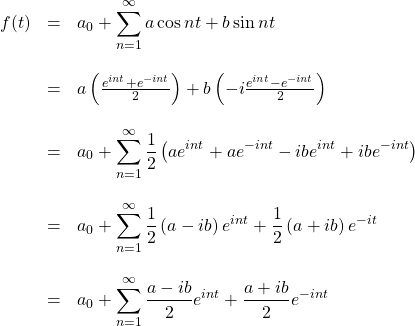
Therefore,
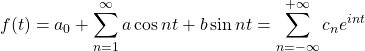 where
where
 is a coefficient (a complex number)
is a coefficient (a complex number) 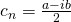 when
when  is positive
is positive when
when 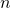 is negative
is negative when
when 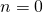
Coefficient derivation
Now we need to find the complex Fourier coefficients in terms of ![]() . The procedure is similar to that used to find the coefficients for the trigonometric Fourier series. We multiply both sides of the complex Fourier series equation by
. The procedure is similar to that used to find the coefficients for the trigonometric Fourier series. We multiply both sides of the complex Fourier series equation by ![]() . We get:
. We get:
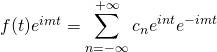
Next, take the definite integral of both sides from ![]() to
to ![]() :
:
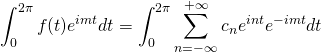
We’ve shown (or at least accepted) previously that ![]() . Therefore, make that change and bring the constant,
. Therefore, make that change and bring the constant, ![]() outside of the integral:
outside of the integral:
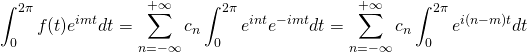
Using Euler’s formula, we know that
![]()
Thus,
![]()
We’ve previously written down, in this article (and proven elsewhere on this site) that
if ![]() then
then
![]() and
and ![]() will both be nonzero
will both be nonzero
![]() and
and ![]()
![]()
if ![]() then
then
![]() and
and ![]()
![]()
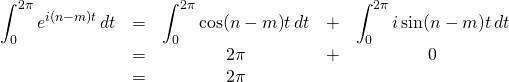
We said that
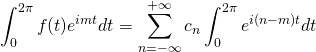
The only term we get from the sum on the righthand side of the equation occurs when ![]() . When this occurs,
. When this occurs, ![]() . All of the other terms in the sum equal zero. Also, when
. All of the other terms in the sum equal zero. Also, when ![]() ,
, ![]() becomes
becomes ![]() . So we wind up with
. So we wind up with
![]()
and
![]()
Fourier Transformation
Derivation of the Fourier transformation
This derivation is taken largely from
Video: Derivation of Fourier Transformation
The trigonometric and complex Fourier series we have been working with are useful in representing periodic functions, i.e., functions that repeat themselves. But how do we represent aperiodic functions, i.e., functions with a period of infinity? We use the Fourier Transformation.
We’ll stick with the complex Fourier representations because they tend to be easier to work with. The complex Fourier series we derived is
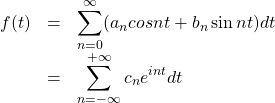
Recall that the argument of sine and cosine functions is an angle. So ![]() represents frequency x time,
represents frequency x time, ![]() being the frequency, either cycles per second or radians per second. We didn’t talk about this earlier, but for the Fourier series to work, the frequencies used to represent a function need to be integer multiples of some base frequency, and that base frequency has to make one cycle during the period of the periodic function we’re trying to estimate. A good explanation of why this can be found in this video:
being the frequency, either cycles per second or radians per second. We didn’t talk about this earlier, but for the Fourier series to work, the frequencies used to represent a function need to be integer multiples of some base frequency, and that base frequency has to make one cycle during the period of the periodic function we’re trying to estimate. A good explanation of why this can be found in this video:
Justification for Fourier series
So the ![]() in the equation for the Fourier series actually means
in the equation for the Fourier series actually means ![]() where
where ![]() is the period of the periodic function we’re trying to represent with our series.
is the period of the periodic function we’re trying to represent with our series.
Let
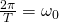 called the primary frequency
called the primary frequency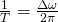 , the difference between primary frequencies that
, the difference between primary frequencies that 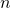 multiplies
multiplies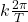 is the overall frequency of the wave where
is the overall frequency of the wave where 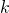 , like
, like 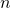 , is an integer
, is an integer
Now if a function is aperiodic, that means the the period of the function is infinity which means that ![]() . As
. As ![]() gets larger and larger:
gets larger and larger:
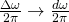
- Sums become integrals
We start off with our Fourier series for ![]()
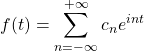
We proved previously that
![]()
We change the limits of integration to the more generic limits ![]() to
to ![]() which allows us to evaluate over a period of any length starting at any point:
which allows us to evaluate over a period of any length starting at any point:
![]()
We combine these 2 equations to get
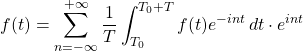
Into this equation, we substitute the values
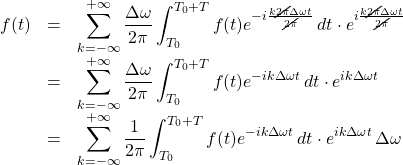
Now we take the limit ![]() . As we noted above, when we do
. As we noted above, when we do
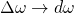
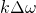 becomes the continuous variable
becomes the continuous variable 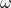
- The summation becomes an integral
In addition, we are saying that our wave never repeats itself. That means that our period extends from ![]() to
to ![]() . Therefore, our limits on the integral change, as follows:
. Therefore, our limits on the integral change, as follows:
![]() and
and ![]()
The results are:
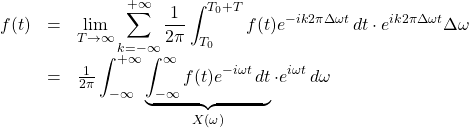
As suggested in the last equation, as ![]() , the expression
, the expression ![]() becomes a continuous function which we’ll call
becomes a continuous function which we’ll call ![]() .
.
We end up with 2 important equations:
Inverse Fourier transformation (also termed the Synthesis equation)
![]()
Forward Fourier transformation (also called the Analysis equation)
![]()
Other forms
There are two other common ways that the Fourier transformation is formulated:
Hertz Frequency
If we work with units of cycles/sec (instead of radians/sec) in our exponentials (i.e., ![]() ), then
), then
- the exponents of our exponential functions would be
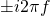 and
and -
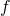 would go to
would go to 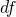 without division by
without division by 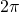 .
.
Therefore, there would be no ![]() outside the integral in the equation for the inverse Fourier transformation
outside the integral in the equation for the inverse Fourier transformation
Our equations would be
![]()
and
![]()
Scaled (Balanced) Version
We can scale the equations we originally derived by multiplying by ![]() by
by ![]() . It would look like this:
. It would look like this:
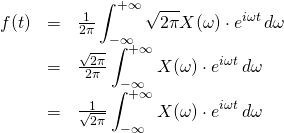
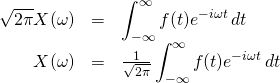
We can apply this scaling factor because, although it effects the absolute amplitudes of ![]() and
and ![]() , the shapes of these functions are unchanged.
, the shapes of these functions are unchanged.
References
https://lpsa.swarthmore.edu/Fourier/Series/DerFS.html
http://www.thefouriertransform.com/series/coefficientsderivation.php
https://npflueger.people.amherst.edu/math19/1201%20Complex%20Fourier%20Series.pdf
