Statement
Consider a function ![]() . Then
. Then
![]()
Proof
This proof is taken from Khan Academy.
To prove the chain rule, we must first prove 2 lemmas:
- If a function is differentiable, then it is also continuous
- If function
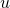 is continuous at
is continuous at 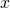 , then
, then 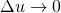 as
as 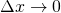
If a function is differentiable, then it is also continuous
By the definition of the derivative:
![]()
A function is continuous at a point, ![]() , if
, if
 is in the domain of
is in the domain of 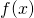
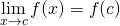
Assume that ![]() is differentiable at
is differentiable at ![]() . Then,
. Then,
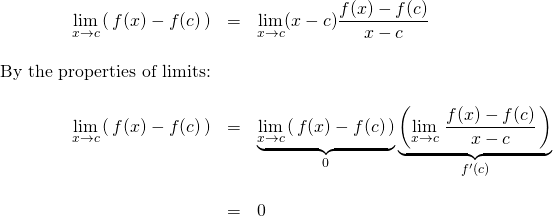
So,
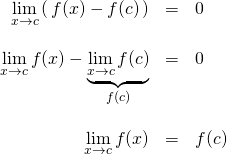
But ![]() , by definition, means that
, by definition, means that ![]() is continuous at
is continuous at ![]() .
.
If function 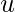 is continuous at
is continuous at 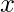 , then
, then 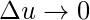 as
as 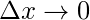
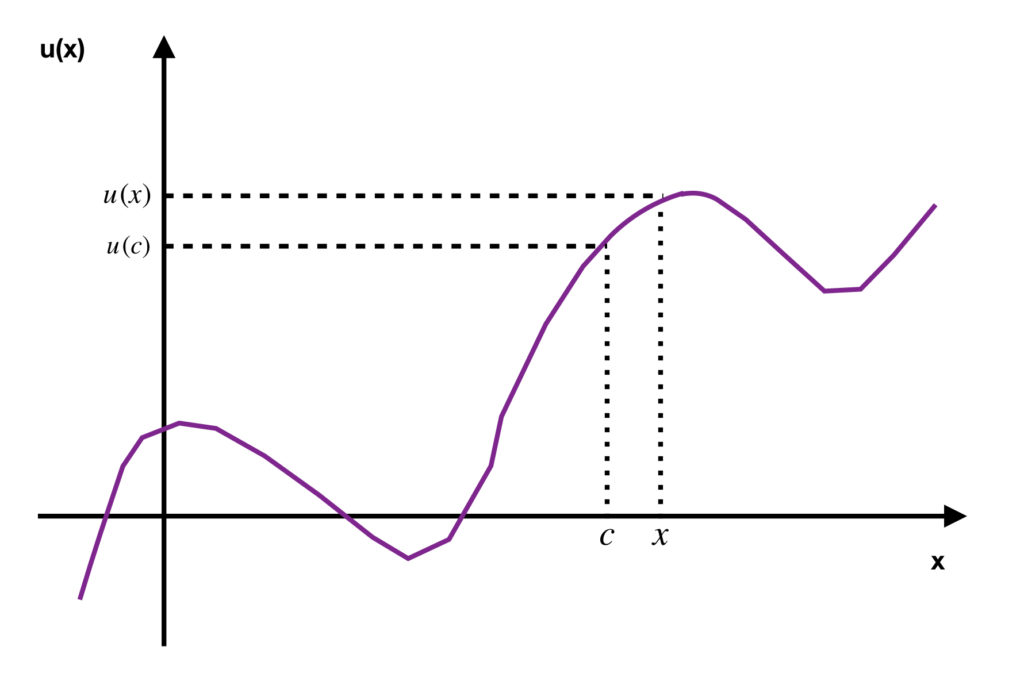
By definition, ![]() is continuous at
is continuous at ![]() if
if
 is in the domain of
is in the domain of 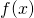
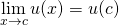
We can rewrite the last equation in a couple of different ways:
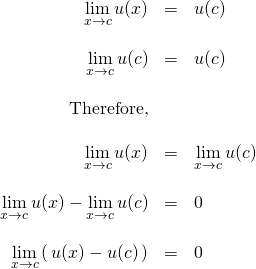
Let
We can substitute these values into the equation ![]() : We get:
: We get:
![]()
This is equivalent to saying that, as ![]() ,
, ![]() , which is what we sought to prove.
, which is what we sought to prove.
Proof of the chain rule
With the background laid, we are now ready to prove the chain rule.
We start by assuming that functions ![]() and
and ![]() are differentiable at
are differentiable at ![]() . We can write the chain rule as:
. We can write the chain rule as:
![]() :
:
By the definition of the derivative:
![]()
Now
![]()
Substituting this into our previous definition of ![]() :
:
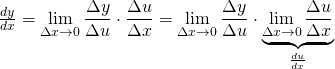
We showed in our proof of our second lemma that, as ![]() ,
, ![]() . We substitute
. We substitute ![]() for
for ![]() in the limit
in the limit ![]() :
:
![]()
But we know what ![]() is; it’s the derivative
is; it’s the derivative ![]() .
.
Thus, we have:
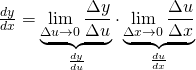
So we end up with
![]()
which is what we wanted to prove.
