Part I
Let ![]() be a continuous real-valued function on a closed interval
be a continuous real-valued function on a closed interval ![]() (closed interval meaning the numbers
(closed interval meaning the numbers ![]() and
and ![]() at the endpoints of the interval are included).
at the endpoints of the interval are included).
Recalling that, by definition,
The area under ![]() from
from ![]() to
to ![]() equals
equals 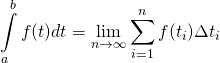 where
where ![]()
Let
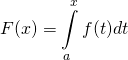
where 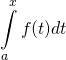 is the area under
is the area under ![]() from
from ![]() to
to ![]() ,
, ![]() being some number between
being some number between ![]() and
and ![]() .
.
Likewise, the area under ![]() between
between ![]() and
and ![]() is:
is:
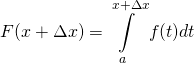
It follows, then, that the area under ![]() from
from ![]() to
to ![]() minus the area under
minus the area under ![]() from
from ![]() to
to ![]() is equal to the area under
is equal to the area under ![]() from
from ![]() to
to ![]() . In mathematical terms:
. In mathematical terms:
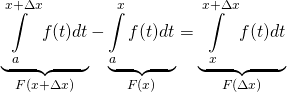
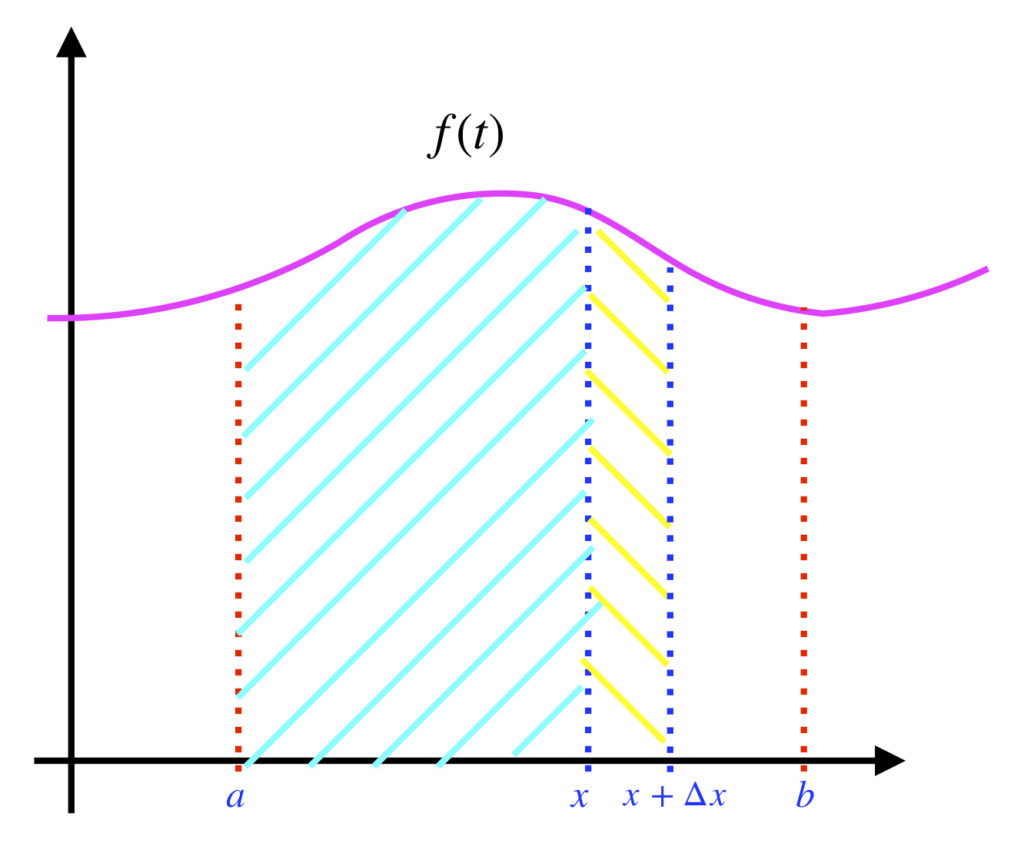
Consider the minimum and maximum values of ![]() between
between ![]() and
and ![]() . Designate them
. Designate them ![]() and
and ![]() , respectively. The area of a rectangle is its base times its height. We know that the area under
, respectively. The area of a rectangle is its base times its height. We know that the area under ![]() on the interval between
on the interval between ![]() and
and ![]() has to be greater than the area of a rectangle with height
has to be greater than the area of a rectangle with height ![]() and base
and base ![]() and less than a rectangle with height
and less than a rectangle with height ![]() and base
and base ![]() . That is,
. That is,
![]()
Next divide through by ![]() . We have:
. We have:
![]()
Now take the limit of this expression as ![]() goes to zero. The following things happen:
goes to zero. The following things happen:
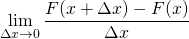 is the definition of the derivative of
is the definition of the derivative of 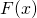 ,
, 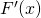
- Because both
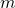 and
and 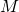 are in the interval between
are in the interval between 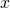 and
and 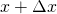 , as
, as 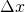 goes to zero, both
goes to zero, both 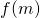 and
and 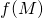 tend toward
tend toward 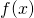 . (This is a result of the squeeze theorem. The intuition behind this theorem can be found here. A formal proof of the theorem can be found here.)
. (This is a result of the squeeze theorem. The intuition behind this theorem can be found here. A formal proof of the theorem can be found here.) - Because
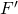 is between
is between 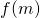 and
and 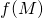 , by the squeeze theorem,
, by the squeeze theorem, 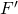 also goes to
also goes to 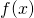 .
.
Thus,
![]()
But
![]()
Therefore,
![]()
The above equation is the fundamental theorem of calculus, part 1.
In the above equations, ![]() is called the antiderivative of
is called the antiderivative of ![]() . Here are some examples:
. Here are some examples:
The term ![]() on the left-hand side of each of the above equations is an arbitrary constant. In each case, we can check the correctness of the above statements by taking the derivative of
on the left-hand side of each of the above equations is an arbitrary constant. In each case, we can check the correctness of the above statements by taking the derivative of ![]() . If we do, we get
. If we do, we get ![]() , the function just to the right of the integral sign and to the left of the differentials
, the function just to the right of the integral sign and to the left of the differentials ![]() and
and ![]() .
.
Why is there a constant, ![]() , added onto every term on the left side of the equations above? It’s because when we take the derivative of the expressions on the left-hand side, the derivative of the non-constant terms gives you
, added onto every term on the left side of the equations above? It’s because when we take the derivative of the expressions on the left-hand side, the derivative of the non-constant terms gives you ![]() and the derivative of the constant term gives you zero. So we could have any constant added to the non-constant term in these expressions and still come out with zero when we take the derivative of that constant. That means that, for any function
and the derivative of the constant term gives you zero. So we could have any constant added to the non-constant term in these expressions and still come out with zero when we take the derivative of that constant. That means that, for any function ![]() that can be integrated, there are an infinite number of antiderivatives which differ only by the constant,
that can be integrated, there are an infinite number of antiderivatives which differ only by the constant, ![]() , that’s added to the end of it.
, that’s added to the end of it.
Part 2
Let ![]() . We know from the first part of the fundamental theorem of calculus that
. We know from the first part of the fundamental theorem of calculus that ![]() . Therefore,
. Therefore, ![]() . That means that
. That means that ![]() is an antiderivative of
is an antiderivative of ![]() as is
as is ![]() . This, in turn, means that
. This, in turn, means that ![]() and
and ![]() differ only by a constant,
differ only by a constant, ![]() .
.
We need to find the value of this constant. To do this, let ![]() . Then,
. Then,
![]() . Why is this zero? Because the we’re taking the area under the curve
. Why is this zero? Because the we’re taking the area under the curve ![]() at one point –
at one point – ![]() . That area is zero.
. That area is zero.
So,
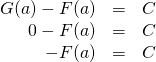
Hence
![]() for all
for all ![]()
In particular,
![]()
But ![]()
Therefore,
![]()
This last equation is the fundamental theorem of calculus, part 2.
