The integral we’re setting out to solve here is the so-called Dirichlet integral:
![]()
We can’t solve this integral by the usual means. There are multiple methods of solving this equation. 5 such methods are outlined at proofwiki. The method we’ll use here is Feynman’s technique. The proof is taken from:
We need to find a way to get the x out of the denominator in the integrand. We do this as follows:
![Rendered by QuickLaTeX.com \begin{align*} \int_0^{\infty}\frac{\sin x }{x} &= \int_0^{\infty}\frac{\sin x }{x}\cdot e^{-0x}\,dx = I(0) \quad \text{(2)} \\ I(b) &= \int_0^{\infty}\frac{\sin x }{x}\cdot e^{-bx}\,dx \quad \text{(3)} \\ \frac{d}{db}[I(b)] &= \frac{\partial}{\partial b}\left( \frac{\sin x }{x}\cdot e^{-bx} \right)\, dx \quad \text{(4)} \\ I^{\prime}(b) &= \frac{\partial}{\partial b}\displaystyle \left(\frac{\sin (x)\,e^{-bx}}{x}\right)\,dx \quad \text{(5)} \\ &= \displaystyle \left(-\frac{\cancel{x}\sin (x)\,e^{-bx}}{\cancel{x}}\right)\,dx \quad \text{(6)} \end{align*}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-b8b0198810ada816695200dd3a7ddc14_l3.png)
Now we’ve got the x out of the denominator of the integrand. Next, we need to integrate ![]() .
.
We use integration by parts twice in a row. Recall, in integration by parts:
![]()
First Integration by Parts:
![]()
![]()
![]()
![]()
So,
![]()
Second Integration by Parts:
![]()
![]()
![]()
![]()
Therefore,
![Rendered by QuickLaTeX.com \begin{align*} \int e^{-bx}\,\sin(x)\,dx &= -\frac{e^{-bx}\sin(x)}{b} - \frac{e^{bx}\cos(x)}{b^2} - \int_0^{\infty} \frac{e^{-bx}\sin(x)}{b^2}\,dx \\ \int \frac{e^{-bx}\sin(x)}{b^2}\,dx + \int e^{-bx}\,\sin(x)\,dx &= -\frac{e^{-bx}\sin(x)}{b} - \frac{e^{bx}\cos(x)}{b^2} \\ \frac{1}{b^2} \cdot \int e^{-bx}\sin(x)\dx + \frac{b^2}{b^2} \cdot \int_0^{\infty} e^{-bx}\,\sin(x)\,dx &= -\frac{e^{-bx}\sin(x)}{b} - \frac{e^{bx}\cos(x)}{b^2} \\ \frac{1 + b^2}{b^2} \cdot \left(\int e^{-bx}\sin(x)\,dx \right) &= -\frac{e^{-bx}\sin(x)}{b} - \frac{e^{bx}\cos(x)}{b^2} \\ \int e^{-bx}\sin(x)\,dx &= \frac{1 + b^2}{b^2} \cdot \left( -\frac{e^{-bx}\sin(x)}{b} - \frac{e^{bx}\cos(x)}{b^2} \right) \\ \int e^{-bx}\sin(x)\,dx &= -\frac{be^{-bx}\sin(x)+e^{bx}\cos(x)}{1 + b^2} \\ \int e^{-bx}\sin(x)\,dx &= -\frac{e^{-bx}(b\sin(x) + \cos(x))}{1 + b^2} \\ \int_0^{\infty} e^{-bx}\sin(x)\,dx &= \eval{[-\frac{e^{-bx}(b\sin(x) + \cos(x))}{1 + b^2}]}_0^{\infty} \\ &= -\frac{e^{-b(\infty)}(b\sin(x) + \cos(x))}{1 + b^2} - -\frac{e^{-b0}(b\sin(0) + \cos(0))}{1 + b^2} \\ &= -\frac{(0)(b\sin(x) + \cos(x))}{1+b^2} + \frac{(1)(0+1)}{1+b^2} \\ &= 0 + \frac{1}{1+b^2} \\ &= \frac{1}{1+b^2} \end{align*}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-10a0b3073a26a75721d05f77ea59a252_l3.png)
In this derivation, to make things simpler, I’ve left off the addition of constants for indefinite integrals and I did the integral of ![]() rather than
rather than ![]() so I have to put the (-) sign back in. Our final result, then, is:
so I have to put the (-) sign back in. Our final result, then, is:
![]()
![]()
We integrate both sides:
![]()
(To see how to get this result, click here.)
Eq. (3) tells us that:
![]()
Thus:
![]()
Take the limit as ![]() :
:
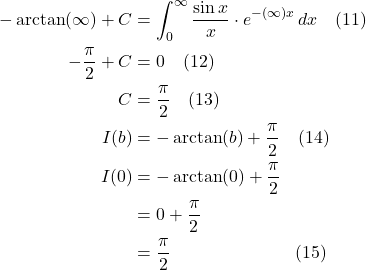
But:
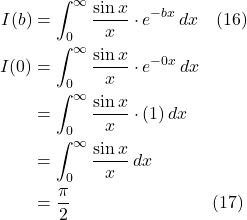
That means that:
![]()
