Contents
Sin(mt)
![]()
Proof
We need to find the antiderivative of ![]() . We know that
. We know that
![]()
So we don’t change the value of our original integral, we need to find a creative way of multiplying that expression by 1. The way to do it is to multiply our original expression by ![]() . We get:
. We get:
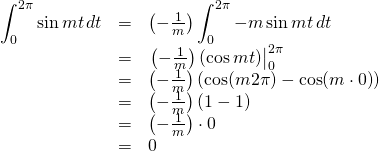
Cos(mt)
![]()
Proof
We need to find the antiderivative of ![]() . We know that
. We know that
![]()
So we don’t change the value of our original integral, we need to find a creative way of multiplying that expression by 1. The way to do it is to multiply our original expression by ![]() . We get:
. We get:
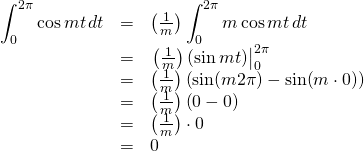
Sin(mt)Cos(nt)
![]()
Proof
We need to make use of the product-to-sum trigonometric identity
![]()
This stems from 2 sum-to-product trigonometric identities, the proofs of which can be found here:
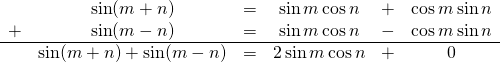
Divide both sides of this last equation by 2. We get
![]()
So,
![Rendered by QuickLaTeX.com \begin{array}{rcl} \displaystyle\int_0^{2\pi}\sin mt \cos nt\,dt &=& \displaystyle\int_0^{2\pi} \frac12\left[ \sin(m+n)+\sin(m-n)\right]\,dt\\ &=& \frac12\displaystyle\int_0^{2\pi}\sin(m+n)\,dt + \frac12\displaystyle\int_0^{2\pi}\sin(m-n)\,dt \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-7053328b98daee85667ac1aa5ac63f61_l3.png)
Since ![]() and
and ![]() are both integers, then
are both integers, then ![]() and
and ![]() are integers. But we proved above that
are integers. But we proved above that
![]()
Therefore,
Thus,
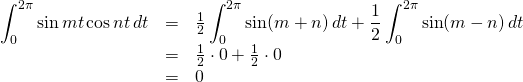
Sin(nt) Sin(mt)
We have 2 things to prove here:
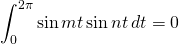 if integers
if integers 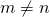 or
or 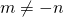
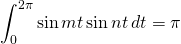 if
if 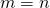
Proof
To prove the above statements, we have to invoke another product-to-sum trigonometric identity:
![]()
This stems from 2 sum-to-product trigonometric identities, the proofs of which can be found here:
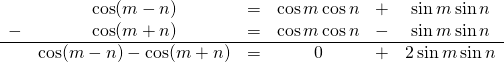
Divide both sides of this last equation by 2. We get
![]()
So,
![Rendered by QuickLaTeX.com \begin{array}{rcl} \displaystyle\int_0^{2\pi}\sin mt \sin nt\,dt &=& \displaystyle\int_0^{2\pi} \frac12\left[ \cos\left((m-n)t)-\cos[(m+n)t\right)\right]\,dt\\ &=& \frac12\displaystyle\int_0^{2\pi}\cos\left((m-n)t\right)\,dt - \frac12\displaystyle\int_0^{2\pi}\cos\left((m+n)t\right)\,dt \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-c82d8ddde515aef62016a6ee8552c251_l3.png)
There are 2 possibilities here. First,
If ![]() then both
then both ![]() and
and ![]() are integers. But we previously proved that
are integers. But we previously proved that
![]()
Therefore,
Thus,
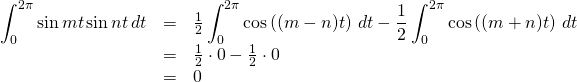
In the second scenario where ![]() ,
, ![]() will still be an integer so the righthand-most term,
will still be an integer so the righthand-most term, ![]() will be 0 and can be ignored.
will be 0 and can be ignored.
However, if ![]() ,
, ![]() . That means that
. That means that
Then
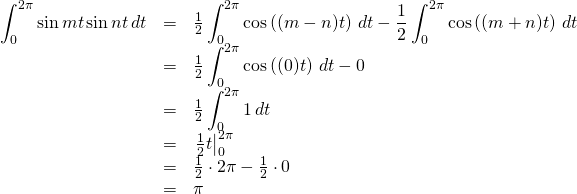
Cos(mt)Cos(nt)
Again, in this case, we have 2 things to prove:
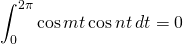 if integers
if integers 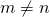 or
or 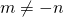
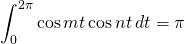 if
if 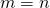
Proof
To prove the above statements, we have to invoke yet another product-to-sum trigonometric identity:
![]()
This stems from 2 sum-to-product trigonometric identities, the proofs of which can be found here:
Divide both sides of this last equation by 2. We get
![]()
So,
![Rendered by QuickLaTeX.com \begin{array}{rcl} \displaystyle\int_0^{2\pi}\cos mt \cos nt\,dt &=& \displaystyle\int_0^{2\pi} \frac12\left[ \cos\left((m-n)t)+\cos[(m+n)t\right)\right]\,dt\\ &=& \frac12\displaystyle\int_0^{2\pi}\cos\left((m-n)t\right)\,dt + \frac12\displaystyle\int_0^{2\pi}\cos\left((m+n)t\right)\,dt \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-055fb076f4b9215ced2ed7c087f3e312_l3.png)
There are 2 possibilities to consider. First,
If ![]() then both
then both ![]() and
and ![]() are integers. But we previously proved that
are integers. But we previously proved that
![]()
Therefore,
Thus,
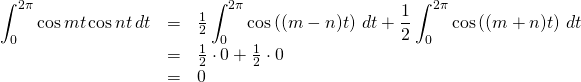
In the second scenario where ![]() ,
, ![]() will still be an integer so the righthand-most term,
will still be an integer so the righthand-most term, ![]() will be 0 and can be ignored.
will be 0 and can be ignored.
However, if ![]() ,
, ![]() . That means that
. That means that
Then

