Contents
Introduction
We want to estimate a function, ![]() , with a power series such that
, with a power series such that
![]() (1)
(1)
and
![]() (2)
(2)
Of course, this will only be true only if the series converges, which can be written mathematically as
![]()
where ![]() is the so-called radius of convergence. This simply means that the series takes on a finite value (as opposed to diverging, which means the value adds to infinity).
is the so-called radius of convergence. This simply means that the series takes on a finite value (as opposed to diverging, which means the value adds to infinity).
Derivation of Taylor Series
As a first approximation, let’s find the value of ![]() and see how it compares with our estimate, which is the right side of equation 1 (we’ll call it
and see how it compares with our estimate, which is the right side of equation 1 (we’ll call it ![]() ). Notice that if we plug
). Notice that if we plug ![]() into the equation, all of the terms that contain
into the equation, all of the terms that contain ![]() will be zero (i.e.,
will be zero (i.e., ![]() ). Therefore,
). Therefore,
![]()
Next let’s check the derivative of ![]() :
:
![]()
If we evaluate ![]() at
at ![]() , all of terms that contain
, all of terms that contain ![]() become zero. Thus, we have
become zero. Thus, we have
![]()
Let’s keep going with the derivatives:
![]()
Evaluate ![]() at
at ![]() . When we do, all of terms that contain
. When we do, all of terms that contain![]() disappear. When we do, we have:
disappear. When we do, we have:
![]()
![]()
Similar to the above calculations, we evaluate ![]() at
at ![]() . As previously, the term with
. As previously, the term with ![]() becomes zero. We are left with
becomes zero. We are left with
![]()
![]()
![]()
We could keep going, but hopefully, the pattern is becoming evident:
The numbers to the left of the coefficients, which are multiplied together and decrease stepwise by 1, are factorials of the subscripts of the coefficients with which they are associated. (Note that the 1 that multiplies ![]() is
is ![]() and
and ![]() also equals 1.) Thus,
also equals 1.) Thus,
and
That means that
 (3)
(3)
Proof that f(x) = P(x) as n → ∞
What we want to do now is to see if
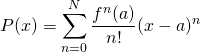 converges to
converges to ![]() as
as ![]() goes to infinity.
goes to infinity.
Remainder function
Let’s start by defining a function, ![]() , called the remainder (sometimes authors call it the error function). It is the difference between our function,
, called the remainder (sometimes authors call it the error function). It is the difference between our function, ![]() , and our Taylor polynomial,
, and our Taylor polynomial, ![]() where our Taylor polynomial contains N derivatives and is centered at the point
where our Taylor polynomial contains N derivatives and is centered at the point ![]() . Alternatively, one might say that it is the error between our function,
. Alternatively, one might say that it is the error between our function, ![]() and the estimate provided by our Taylor polynomial,
and the estimate provided by our Taylor polynomial, ![]() at some point
at some point ![]() . In equation form,
. In equation form,
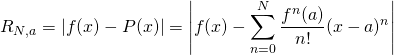
What we want to know is, what is the remainder at some point ![]() remote from
remote from ![]() (
(![]() , again, being the point on which are Taylor polynomial is derived).
, again, being the point on which are Taylor polynomial is derived).
What we already know is that ![]() estimates
estimates ![]() perfectly at
perfectly at ![]() . Therefore,
. Therefore,
![]()
Next, let’s take the derivative of the function above:
![]()
The difference in the derivatives is 0 because, as we saw when we derived the expression for the Taylor series, the derivatives of ![]() are equal to the derivatives of
are equal to the derivatives of ![]() for all levels of derivative up to
for all levels of derivative up to ![]() . That is,
. That is,
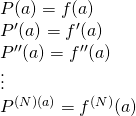
Because of this,
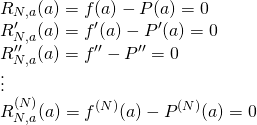
Now let’s take the ![]() derivative of the above equation:
derivative of the above equation:
![]()
To solve this equation, we focus specifically on the term ![]() . Note that a subscript,
. Note that a subscript, ![]() has been added to this term to emphasize that
has been added to this term to emphasize that ![]() is an
is an ![]() degree polynomial. What is its value? Zero. Why? Because the
degree polynomial. What is its value? Zero. Why? Because the ![]() derivative of an
derivative of an ![]() degree polynomial is zero. (For example, if
degree polynomial is zero. (For example, if ![]() ,
, ![]() ,
, ![]() and
and ![]() .) Due to this,
.) Due to this,
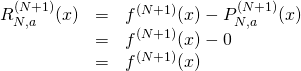
The next thing we need to do is try to find an upper bound to ![]() (we’ll call it
(we’ll call it ![]() ). In math terms,
). In math terms,
![]()
We take the absolute values of ![]() and
and ![]() because our error could be positive or negative but what we care about is the magnitude of the error.
because our error could be positive or negative but what we care about is the magnitude of the error.
Now we know that, because ![]() , like all the functions we’ve been dealing with in this article, is continuous, then, on the interval from
, like all the functions we’ve been dealing with in this article, is continuous, then, on the interval from ![]() to
to ![]() , it must have a maximum value. And we already said that we are going to call that maximum value (or upper bound)
, it must have a maximum value. And we already said that we are going to call that maximum value (or upper bound) ![]() .That means that,
.That means that,
![]()
And because ![]() ,
,
![]()
What we want to prove, though, is that,
![]()
So somehow, we’ve got to get from the ![]() derivative of
derivative of ![]() to the “zeroth” derivative of
to the “zeroth” derivative of ![]() (i.e., the zeroth derivative being the function,
(i.e., the zeroth derivative being the function,![]() , itself). How do we do this? By successive integrations. Let’s start with
, itself). How do we do this? By successive integrations. Let’s start with
![]()
Before we proceed with this undertaking, let us consider an important aside: namely that
![]()
If the area under both curves are either both positive or both negative, then their areas will be equal. However, if part of the area is positive and part is negative, then, with ![]() , the negative part will cancel out the positive part of the area. On the other hand, with the absolute value sign on the inside of the integral, the negative part of the area, because of this absolute value sign, will add positively to the positive portion of the area rather than being subtracted from it. Thus,
, the negative part will cancel out the positive part of the area. On the other hand, with the absolute value sign on the inside of the integral, the negative part of the area, because of this absolute value sign, will add positively to the positive portion of the area rather than being subtracted from it. Thus, ![]() potentially has a higher value than
potentially has a higher value than ![]() .
.
With that aside behind us, let’s move on to the successive integration process. To begin
![]() and
and ![]() where
where ![]() is a constant made up from contributions of the indefinite integrals on both sides of the equation. Therefore,
is a constant made up from contributions of the indefinite integrals on both sides of the equation. Therefore,
![]()
Since we want to find the lowest upper bound for our error function, we want to minimize ![]() . We’ve already established that
. We’ve already established that ![]() so
so ![]() . That means that
. That means that ![]() and
and ![]() . Thus, we have
. Thus, we have
![]()
We integrate both sides of this equation:
![]()
We get
![]()
To minimize the constant ![]() , we use the same trick we used above; we take the value of both sides of this equation at
, we use the same trick we used above; we take the value of both sides of this equation at ![]() . So,
. So,
![]() . Because the right side of the equation will contain an
. Because the right side of the equation will contain an ![]() term in all of our subsequent integration steps, the constant
term in all of our subsequent integration steps, the constant ![]() will be 0 in all of these steps. Thus, we can ignore the constant from here on out.
will be 0 in all of these steps. Thus, we can ignore the constant from here on out.
We continue our successive integration process as follows:

From this, we can come up with an expression for ![]() at
at ![]() :
:
![]()
We can use this expression to prove that ![]() converges to
converges to ![]() over some interval of
over some interval of ![]() . Note that this interval can be infinite in some cases
. Note that this interval can be infinite in some cases
Example: ex
The exponential function, ![]() , is ubiquitously useful in science and mathematics. Therefore, it will be useful to examine it further. The first order of business is to derive it’s Taylor series. Toward this end, we’ll construct a table:
, is ubiquitously useful in science and mathematics. Therefore, it will be useful to examine it further. The first order of business is to derive it’s Taylor series. Toward this end, we’ll construct a table:
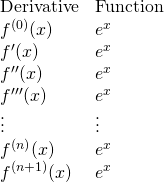
This table illustrates that, of the exponential function, the function itself and all of its derivatives are equal to ![]() .
.
The general formula for the Taylor series is:
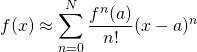
For this proof, we’re going to use the specialized form of the Taylor series called the Maclaurin series in which the series is centered at zero (i.e., ![]() ). The formula is:
). The formula is:
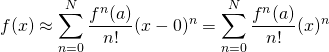
We know that ![]() and all its derivatives are equal to
and all its derivatives are equal to ![]() . We also know that
. We also know that ![]() . So now lets plug this information into the formula for the Maclaurin series:
. So now lets plug this information into the formula for the Maclaurin series:
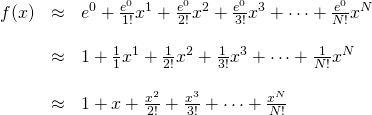
Now we want to show that the above Maclaurin series converges to ![]() for the interval
for the interval ![]() . To do this, we use Taylor’s inequality and the remainder function that we previously derived.
. To do this, we use Taylor’s inequality and the remainder function that we previously derived.
We know that the ![]() derivative of
derivative of ![]() , like all of its derivatives, is
, like all of its derivatives, is ![]() . Therefore, the maximum value of
. Therefore, the maximum value of ![]() on the interval
on the interval ![]() is
is ![]() .
. ![]() , then, is the value of
, then, is the value of ![]() in the formula for Taylor’s inequality. Because, in this case, we’re taking
in the formula for Taylor’s inequality. Because, in this case, we’re taking ![]() ,
, ![]() . Thus, for Taylor’s inequality, we have
. Thus, for Taylor’s inequality, we have
![]()
Finally, we take the limit as ![]() of both sides. That gives us
of both sides. That gives us
![]()
because ![]() goes to infinity much faster than
goes to infinity much faster than ![]() . To see this, plug in some values of
. To see this, plug in some values of ![]() at
at ![]() :
:
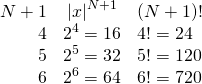
Since ![]() , the error between
, the error between ![]() and
and ![]() , goes to 0 as
, goes to 0 as ![]() , that means that
, that means that ![]() , as
, as ![]() . And because
. And because ![]() for any
for any ![]() we choose, that means that
we choose, that means that ![]() equals its Taylor series at all values of
equals its Taylor series at all values of ![]() .
.
Example: sin x
Next let’s calculate the Maclaurin series for ![]() ,
, ![]() , and prove that
, and prove that ![]() as
as ![]() .
.

We use this data to calculate the Maclaurin series of ![]() :
:
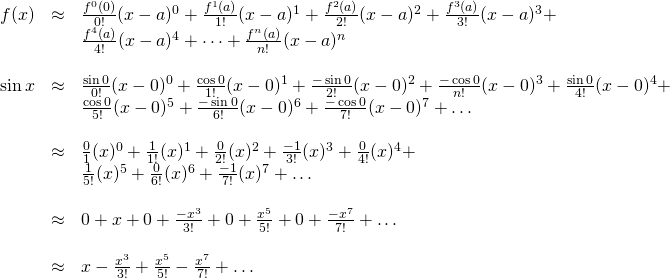
Now we prove that the Maclaurin series for ![]() converges to
converges to ![]() as
as ![]() . We’ll set the interval of convergence to
. We’ll set the interval of convergence to ![]() (i.e., one complete cycle). Because
(i.e., one complete cycle). Because ![]() is a periodic function, in so doing, whatever we prove will hold for all
is a periodic function, in so doing, whatever we prove will hold for all ![]() .
.
Note that the derivatives of ![]() consist of
consist of ![]() and
and ![]() .
. ![]() and
and ![]() vary between -1 and +1. Thus,
vary between -1 and +1. Thus, ![]() . So we have
. So we have
![]()
Therefore, the Maclaurin series of ![]() converges to
converges to ![]() for all values of
for all values of ![]() .
.
Example: cos x
In this section, we’ll calculate the Maclaurin series for ![]() ,
, ![]() , and prove that
, and prove that ![]() as
as ![]() .
.

We use this data to calculate the Maclaurin series of ![]() :
:
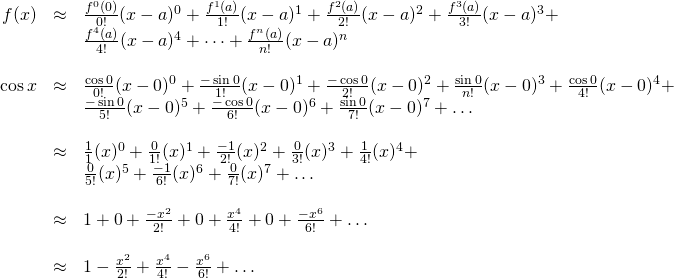
Now we prove that the Maclaurin series for ![]() converges to
converges to ![]() as
as ![]() . We’ll set the interval of convergence to
. We’ll set the interval of convergence to ![]() (i.e., one complete cycle). Because
(i.e., one complete cycle). Because ![]() is a periodic function, in so doing, whatever we prove will hold for all
is a periodic function, in so doing, whatever we prove will hold for all ![]() .
.
Note that the derivatives of ![]() consist of
consist of ![]() and
and ![]() .
. ![]() and
and ![]() vary between -1 and +1. Thus,
vary between -1 and +1. Thus, ![]() . So we have
. So we have
![]()
Therefore, the Maclaurin series of ![]() converges to
converges to ![]() for all values of
for all values of ![]() .
.
References
http://ocw.uci.edu/lectures/math_2b_lec_27_calculus_taylor_series_and_maclaurin_series.html
