There are a number of definitions of the exponential function, ![]() . However, there are 3 main ones:
. However, there are 3 main ones:
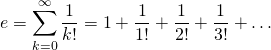
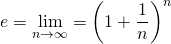
 is the positive real number such that
is the positive real number such that 
Here is a proof of #1:
We showed elsewhere on this site that the Taylor series representation of ![]() equals
equals ![]() for all
for all ![]() . This representation is as follows:
. This representation is as follows:
![]()
But ![]() . Thus,
. Thus, ![]() . The limit shown above then becomes:
. The limit shown above then becomes:
![]()
The following link provides an intuitive explanation then a formal proof of #2:
http://www.milefoot.com/math/calculus/limits/LimitDefinitionOfE10.htm
The following link provides a proof that the 3 definitions of ![]() listed above are equivalent:
listed above are equivalent:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.165.3459&rep=rep1&type=pdf
To understand this proof, videos from series on combinatorics and the binomial theorem taken from Khan Academy may be helpful:
