Coordinate Transformations – Sam Artigliere's Blog

Polar Coordinates
Cylindrical Coordinates
Spherical Coordinates
Vector components in rotated Cartesian coordinates
Basis vector rotation in Cartesian coordinates

Polar Coordinates

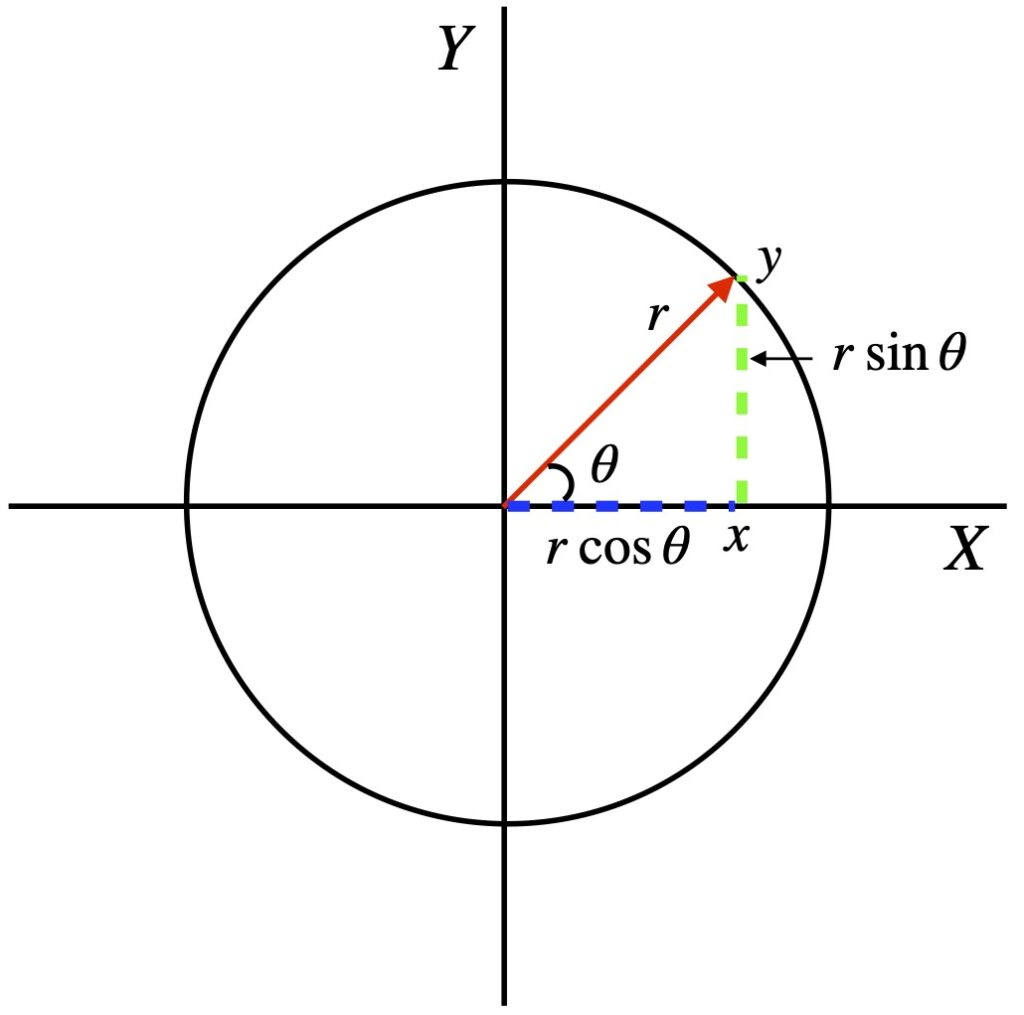
Coordinates

$x=r\cos\theta$
$y=r\sin\theta$

$r=\sqrt{x^2+y^2}$
$\displaystyle \theta=\arctan \frac{y}{x}$

Basis Vectors

We can define the vector $\vec{r}$ in terms of Cartesian basis vectors:

$\vec{r} = x\,\hat{x} + y\,\hat{y}$
$=r\cos\theta\, \hat{x} + r\sin\theta\, \hat{y}$

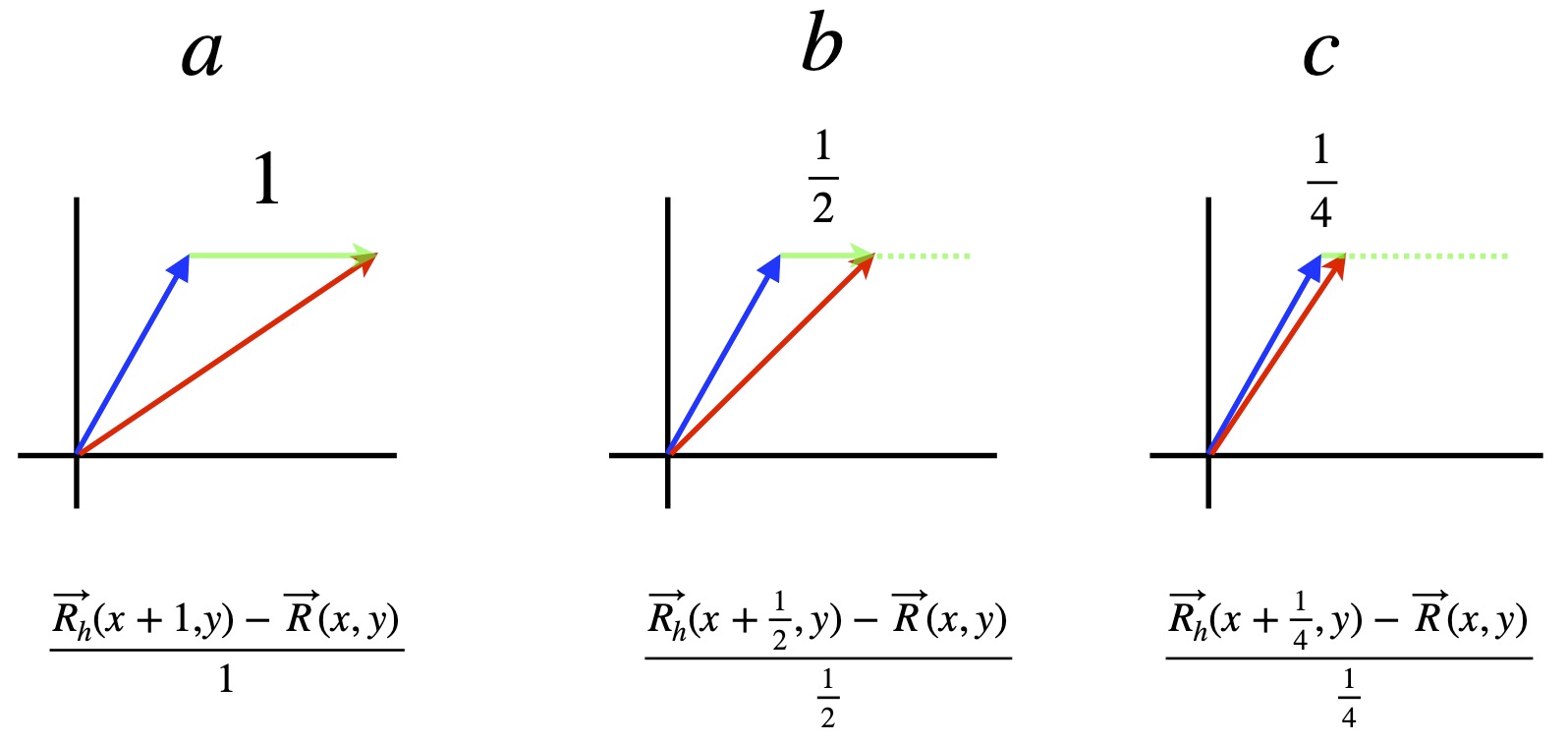
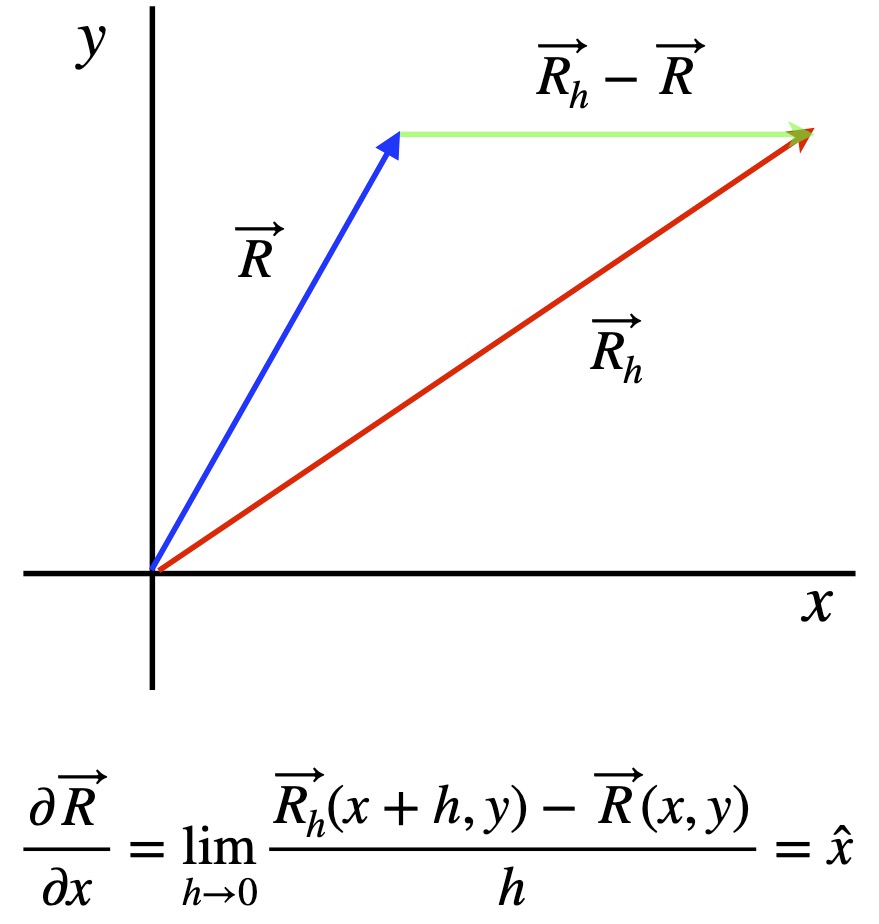
We express any basis vector as a partial derivative:

$\vec{e}_u = \displaystyle \frac{\partial \vec{r}}{\partial u}$

$\vec{e}_u$ is a vector tangent to $\vec{r}$ in the u direction. If we want to get a unit vector, we need to normalize $\vec{e}_u$ by dividing it by $\lvert\ \vec{e}_u\rvert$ .

To see why, $\vec{e}_u = \displaystyle \frac{\partial \vec{r}}{\partial u}$ click :

Applying this to eq (), we get:

$\displaystyle \hat{e}_r = \displaystyle \frac{\partial \vec{r}}{\partial r}=\frac{\partial\left[r(\cos\theta\, \hat{x} + \sin\theta\, \hat{y})\right]}{\partial r}$
$=\cos\theta\, \hat{x} + \sin\theta\, \hat{y}$

and

$\displaystyle \hat{e}_{\theta} = \displaystyle \frac{\partial \vec{r}}{\partial \theta}=\frac{\partial\left[r(\cos\theta\, \hat{x} + \sin\theta\, \hat{y})\right]}{\partial \theta}$
$=-r\sin\theta\, \hat{x} + r\cos\theta\, \hat{y}$

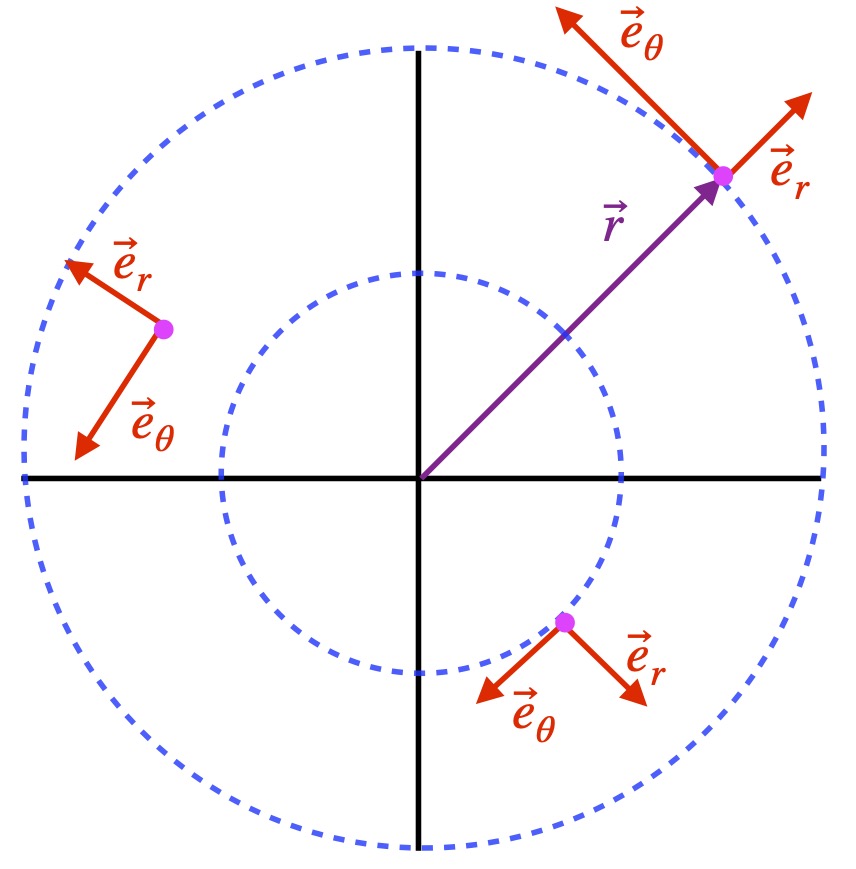
Notice that, unlike the Cartesian basis vectors $\hat{x}$ and $\hat{y}$ , which are the same length and point in the same direction elsewhere, polar basis vectors vary. Specifically:

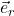$\vec{e}_r$ varies in direction with 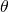$\theta$ but is constant in length.
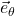$\vec{e}_{\theta}$ also varies its direction with 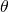$\theta$ . However, in addition, its length scales with $r$ .

If we’re working with a unit circle i.e., $r=1$ , then we can ignore the $r$ in our equation for $\vec{e}_{\theta}$ . However, $\vec{e}_{\theta}$ scales with $r$ . Note that some authors normalize the expression for $\vec{e}_{\theta}$ by dividing by $r$ .

It’s also easy to show that $\vec{e}_r$ and $\vec{e}_{\theta}$ are orthogonal. By definition, vectors are orthogonal if their dot product equals zero. For $\vec{e}_r$ and $\vec{e}_{\theta}$ , we have:

$\vec{e}_r \cdot \vec{e}_{\theta} = (\cos\theta )(-r\sin\theta) + (\sin\theta)(r\cos\theta) = 0$

Figure X is designed to provide visual intuition about why basis vectors in polar coordinates are what they are. Figure Xb is a blow-up of the area in figure Xa enclosed in the dotted blue circle. In this figure, we’re assuming that all basis vectors are normalized.

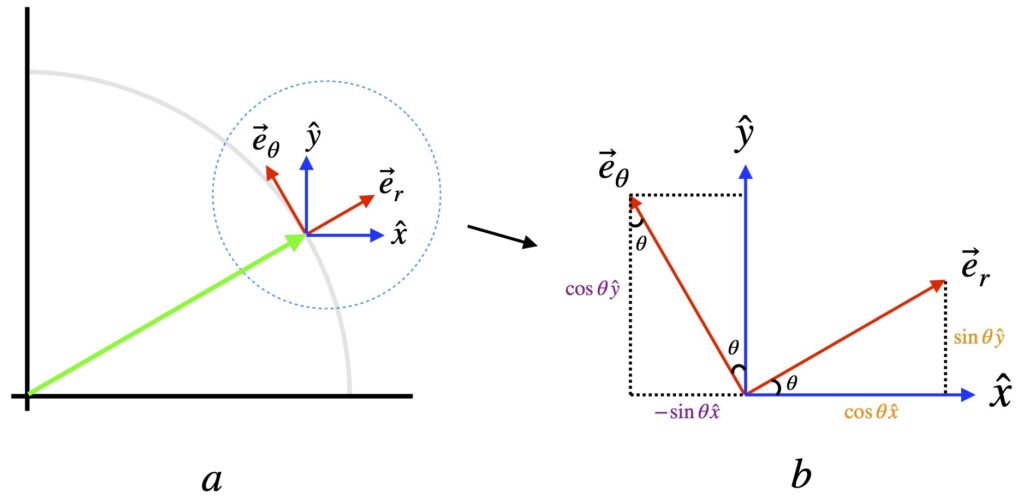
Blow-up of basis vectors in polar coordinates

We can express Cartesian basis vectors in terms of polar basis vector, as follows:

$\hat{x} = \hat{e}_r\,\cos\theta -\hat{e}_{\theta}\,\sin\theta$
$\hat{y} = \hat{e}_r\,\sin\theta + \hat{e}_{\theta}\,\cos\theta$

Figure X may be helpful to understand these equations better.

Conversion of polar basis vector to Cartesian basis vectors

Line Element

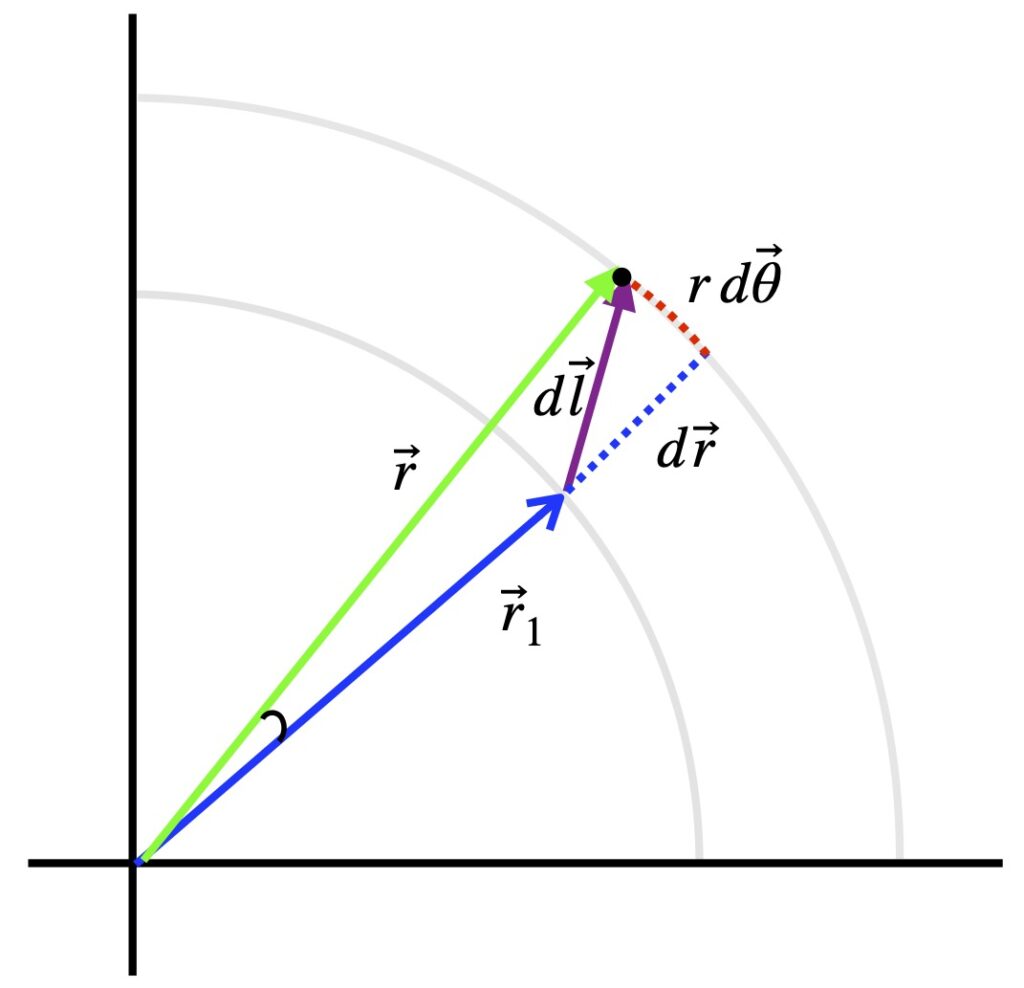
Anticipating derivation of the metric in polar coordinates, this section is designed to determine the line element in polar coordinates.

Referring to figure X (obviously not drawn to scale), we seek to find the infinitesimal displacement vector, $d\vec{l}$ , as we move radially outward and counterclockwise from the tip of $\vec{r}_1$ to the tip of $\vec{r}$ . The radial component is just $d\vec{r}$ . The component in the direction of $\theta$ is the arc length between the outer tip of $d\vec{r}$ and the outer tip of $\vec{r}$ which, in general, is the product of the radius times the angle $\theta$ in radians. Thus, we can write:

$d\vec{l} = dr\,\hat{e}_r + r\,d\theta\,\hat{e}_{\theta}$

The line element, which is the length of the infinitesimal displacement vector – like the length of any vector – is given by the dot product of the infinitesimal displacement vector with itself. In polar coordinates, then, the line element is:

$ds^2 = d\vec{l} \cdot d\vec{l} = dr^2 + r^2 d\theta^2$

Cylindrical Coordinates

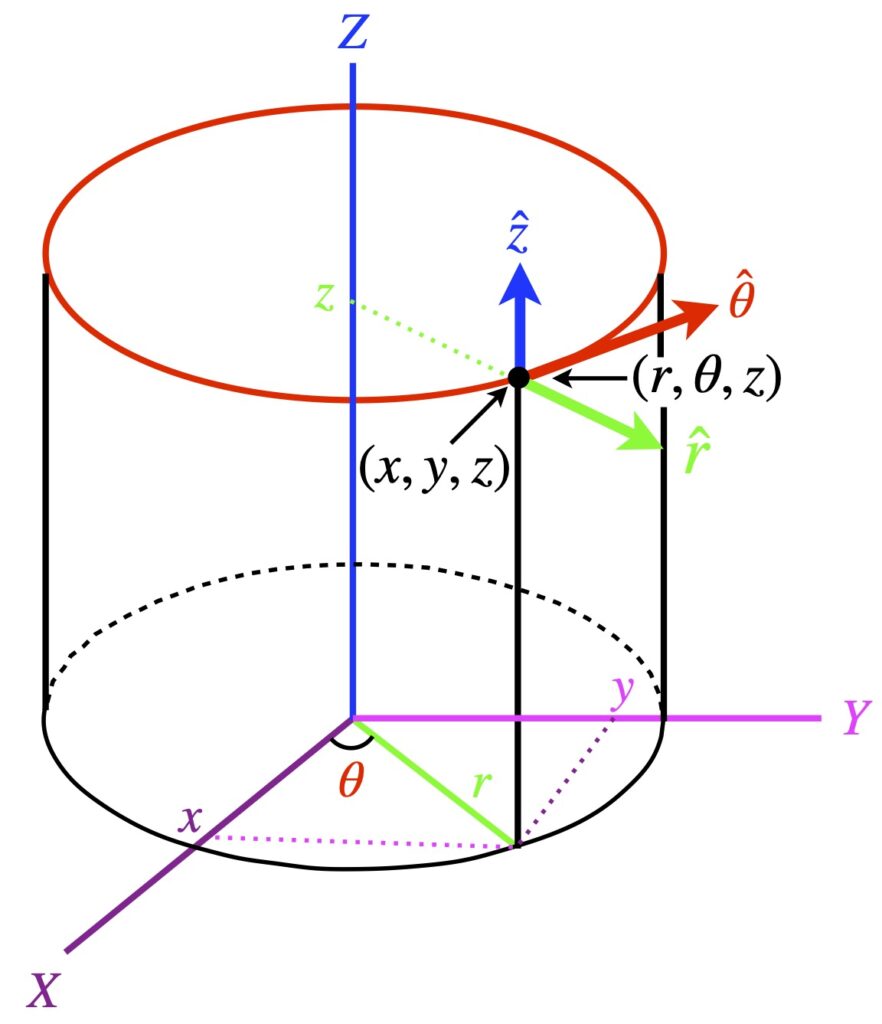
Cylindrical coordinates are similar to polar coordinates but with the addition of a z-coordinate that is equal to the Cartesian z-coordinate. Because I’ve gone through derivations for polar coordinates in the previous section, I won’t repeat them; instead, I’ll just catalogue the results.

Coordinates

$x=r\cos\theta$
$y=r\sin\theta$
$z=z$

$r=\sqrt{x^2 + y^2}$
$\theta=\arctan\displaystyle \frac{y}{x}$
$z=z$

Basis Vectors

Polar basis vectors in terms of Cartesian basis vectors:

$\hat{e}_r = \cos\theta\,\hat{x} + \sin\theta\,\hat{y}$
$\hat{e}_{\theta} = -\sin\theta\,\hat{x} + \cos\theta\,\hat{y}$
$\hat{z}=\hat{z}$

Cartesian basis vectors in terms of Polar basis vectors:

$\hat{x}= \cos\theta\,\hat{e}_r - \sin\theta\,\hat{e}_{\theta}$
$\hat{y} = \sin\theta\,\hat{e}_r + \cos\theta\,\hat{e}_{\theta}$
$\hat{z}=\hat{z}$

Line Element

$ds^2 = dr^2 + r^2 d\theta^2 + dz^2$

Spherical Coordinates

Coordinates

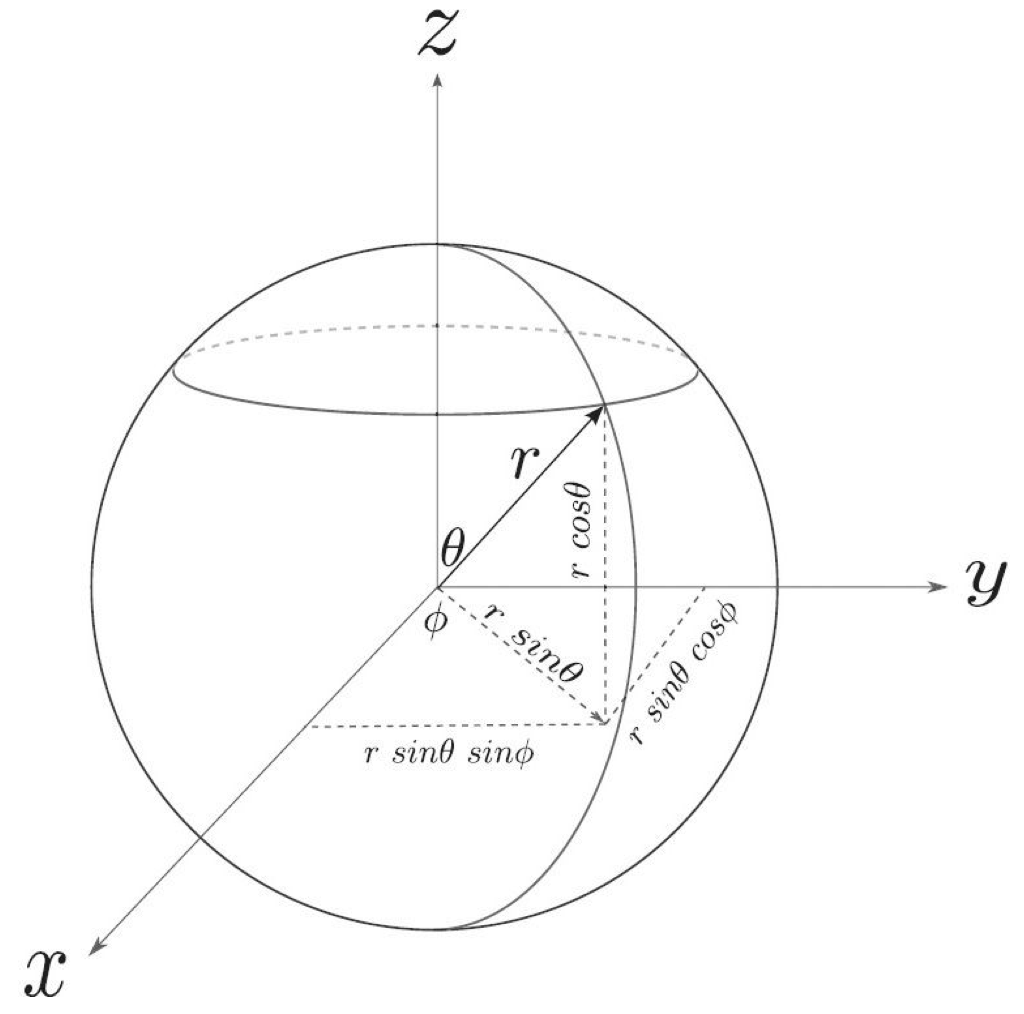
From figure X, we glean that:

$x=r\sin\theta\cos\phi$
$y=r\sin\theta\sin\phi$
$z=r\cos\theta$

Basis Vectors

We can describe the vector $\vec{r}$ as follows:

$\vec{r}=x\,\hat{x} + y\,\hat{y} + z\,\hat{z}$

Substituting the coordinate conversions from the last section, we have:

$\vec{r}=r\sin\theta\cos\phi\,\hat{x} + r\sin\theta\sin\phi\,\hat{y} + r\cos\theta\,\hat{z}$
$=r(\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z})$

Back in our derivation of polar basis vectors, we discovered that

$\vec{e}_u = \displaystyle \frac{\partial \vec{r}}{\partial u}; \quad \hat{e}_u=\frac{\vec{e}_u}{\lvert \vec{e}_u \rvert}$

We make use of these relationships to find each of the spherical coordinate basis vectors: $\hat{e}_r$ , $\hat{e}_{\theta}$ and $\hat{e}_{\phi}$ We’ll start with $\hat{e}_r$ .

$\vec{e}_r=\displaystyle \frac{\partial \vec{r}}{\partial r}$

$=\displaystyle \frac{\partial \left[r(\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z})\right]}{\partial r}$

$=\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z}$

To normalize $\vec{e}_r$ , we have to divide by $\lvert \vec{e}_r \rvert$ :

$\lvert \vec{e}_r \rvert=\vec{e}_r \cdot \vec{e}_r = \sqrt{\sin^2\theta\cos^2\phi + \sin^2\theta\sin^2\phi + \cos^2\theta}$

$=\sqrt{\sin^2\theta(\cos^2\phi + \sin^2\phi)+\cos^2\theta}$

$=\sqrt{\sin^2\theta + \cos^2\theta}$

$=\sqrt{1}$

$=1$

So,

$\hat{e}_r=\displaystyle \frac{\vec{r}}{\lvert \vec{e}_r \rvert}$

$=\displaystyle \frac{\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z}}{1}$

$=\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z}$

Deriving $\hat{e}_{\theta}$ and $\hat{e}_{\phi}$ are a bit more involved. Next we’ll look at $\hat{e}_{\theta}$ .

$\vec{e}_{\theta}=\displaystyle \frac{\partial \vec{r}}{\partial \theta}$

$=\displaystyle \frac{\partial \left[r(\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z})\right]}{\partial \theta}$

$=\displaystyle r(\cos\theta\cos\phi\,\hat{x} + \cos\theta\sin\phi\,\hat{y} - \sin\theta\,\hat{z})$

To normalize $\vec{e}_{\theta}$ we need to divide it by its length. Thus,

$\lvert \vec{e}_{\theta} \rvert=\sqrt{r^2(\cos^2\theta\cos^2\phi + \cos^2\theta\sin^2\phi + \sin^2\theta)}$

$=\sqrt{r^2\left[\cos^2\theta(\cos^2\phi + \sin^2\phi) + \sin^2\theta\right]}$

$=\sqrt{r^2\left[\cos^2\theta + \sin^2\theta\right]}$

$=\sqrt{r^2}$

$=r$

That means that:

$\hat{e}_{\theta}=\displaystyle \frac{\vec{e}_{\theta}}{\lvert \vec{e}_{\theta} \rvert}$

$=\displaystyle \frac{r(\cos\theta\cos\phi\,\hat{x} + \cos\theta\sin\phi\,\hat{y} - \sin\theta\,\hat{z})}{r}$

$=\cos\theta\cos\phi\,\hat{x} + \cos\theta\sin\phi\,\hat{y} - \sin\theta\,\hat{z}$

Finally, we’ll derive $\hat{e}_{\phi}$ . We begin with:

$\vec{e}_{\phi} = \displaystyle \frac{\partial \vec{r}}{\partial \phi}$

$=\displaystyle \frac{\partial \left[r(\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z})\right]}{\partial \phi}$

$=\displaystyle r(-\sin\theta\sin\phi\hat{x} + \sin\theta\cos\phi\hat{y})$

$=r\sin\theta(- \sin\phi\hat{x} + \cos\phi\hat{y})$

To normalize $\vec{e}_{\phi}$ , we need to divide it by its length. We get the length as follows:

$\lvert \vec{e}_{\phi} \rvert=\sqrt{r^2(\sin^2\theta\sin^2\phi + \sin^2\theta)\cos^2\phi) }$

$=\sqrt{r^2\sin^2\theta(\sin^2\theta + \cos^2\theta)}$

$=\sqrt{r^2\sin^2\theta}$

$=r\sin\theta$

And dividing by that length, we get:

$\hat{e}_{\phi}=\displaystyle \frac{\vec{e}_{\phi}}{\lvert \vec{e}_{\phi} \rvert}$

$=\displaystyle \frac{r\sin\theta(- \sin\phi\hat{x} + \cos\phi\hat{y})}{r\sin\theta}$

$=- \sin\phi\hat{x} + \cos\phi\hat{y}$

To summarize, the basis vectors in spherical coordinates are:

$\hat{e}_r=\sin\theta\cos\phi\,\hat{x} + \sin\theta\sin\phi\,\hat{y} + \cos\theta\,\hat{z}$
$\hat{e}_{\theta}=\cos\theta\cos\phi\,\hat{x} + \cos\theta\sin\phi\,\hat{y} - \sin\theta\,\hat{z}$
$\hat{e}_{\phi}=- \sin\phi\hat{x} + \cos\phi\hat{y}$

The last thing I’d like to do in this section is prove that the spherical coordinate basis vectors are orthogonal. To do this, we show that the dot products of the basis vectors equals zero.

$\hat{e}_r\cdot\hat{e}_{\phi} =\sin\theta\cos\theta\cos^2\phi + \sin\theta\cos\theta\sin^2\phi+ -\sin\theta\cos\theta$
$=\sin\theta\cos\theta(\cos^2\phi+\sin^2\phi)-\sin\theta\cos\theta$
$=\sin\theta\cos\theta-\sin\theta\cos\theta$
$=0$

$\hat{e}_r\cdot\hat{e}_{\theta} =-\sin\theta\cos\phi\sin\phi + \sin\theta\cos\phi\sin\phi = 0$

$\hat{e}_{\theta}\cdot\hat{e}_{\phi}=-\cos\theta\cos\theta\sin\phi + \cos\theta\sin\phi\cos\phi = 0$

Line Element

We’ll first derive the line element in spherical coordinates by a method I’ll call the algebraic method.

In Cartesian coordinates, the line element is:

$ds^2=dx^2+dy^2+dz^2$

We know that:

$x=r\sin\theta\cos\phi$
$y=r\sin\theta\sin\phi$
$z=r\cos\theta$

The total derivative is defined as:

$df=\displaystyle \frac{\partial f}{\partial x^1}dx^1+\frac{\partial f}{\partial x^2}dx^2+\dots+\frac{\partial f}{\partial x^n}dx^n$

Using this on eq (), we have:

$dx=\sin\theta\cos\phi dr+ r\cos\theta\cos\phi d\theta - r\sin\theta\sin\phi d\phi$
$dy=\sin\theta\sin\phi dr + r\cos\theta\sin\phi d\theta + r\sin\theta\cos\phi d\phi$
$dz=\cos\theta dr - r\sin\theta d\theta$

Then

$ds^2=dx^2+dy^2+dz^2$
$=(\sin\theta\cos\phi dr+ r\cos\theta\cos\phi d\theta - r\sin\theta\sin\phi d\phi)^2$
$+(\sin\theta\sin\phi dr + r\cos\theta\sin\phi d\theta + r\sin\theta\cos\phi d\phi)^2$
$+(\cos\theta dr - r\sin\theta d\theta)^2$

Note that the squared terms in the equation above actually represent the dot product with itself (e.g., $dy^2$ really means $dy\cdot dy$ . I’ve used the squared shorthand to save space, in the equation above and in the equations that follow in this section.

We showed, in the last section, that the spherical coordinate basis vectors are orthogonal. Therefore, terms multiplied by $dr\,d\theta$ , $dr\,d\phi$ and $d\theta\,d\phi$ will all be zero. The only terms that survive are the $dr^2$ , $d\theta^2$ and $d\phi^2$ terms.

For the ${dr^2}$ term:

$=(\sin^2\theta\cos^2\phi + \sin^2\theta\sin^2\phi + \cos^2\theta)dr^2$
$=\left[\sin^2\theta(\cos^2\phi+\sin^2\phi)+\cos^2\theta\right]dr^2$
$=(\sin^2\theta+\cos^2\theta)dr^2$
$=dr^2$

For the ${d\theta^2}$ term:

$=(r^2\cos^2\theta\cos^2\phi + r^2\cos^2\theta\sin^2\phi + r^2\sin^2\theta)d\theta^2$
$=r^2(\cos^2\theta\cos^2\phi + \cos^2\theta\sin^2\phi + \sin^2\theta)d\theta^2)d\theta^2$
$=\left[r^2(\cos^2\theta(\cos^2\phi+\sin^2\phi)) + \sin^2\theta\right]d\theta^2$ $=\left[r^2(\cos^2\theta + \sin^2\theta\right]d\theta^2$ $=r^2\,d\theta^2$

For the ${d\phi^2}$ term:

$=(r^2\sin^2\theta\sin^2\phi + r^2\sin^2\theta\cos^2\phi)d\phi^2$
$=r^2\sin^2\theta(\sin^2\phi + \cos^2\phi)d\phi^2$
$=r^2\sin^2 \theta\,d\phi^2$

So the line element we’re left with is:

$ds^2 = dr^2 + r^2\,d\theta^2 + r^2\sin^2\theta\,d\phi^2$

We can gain further intuition as to why the line element for spherical coordinates are what they are by examining figure X.

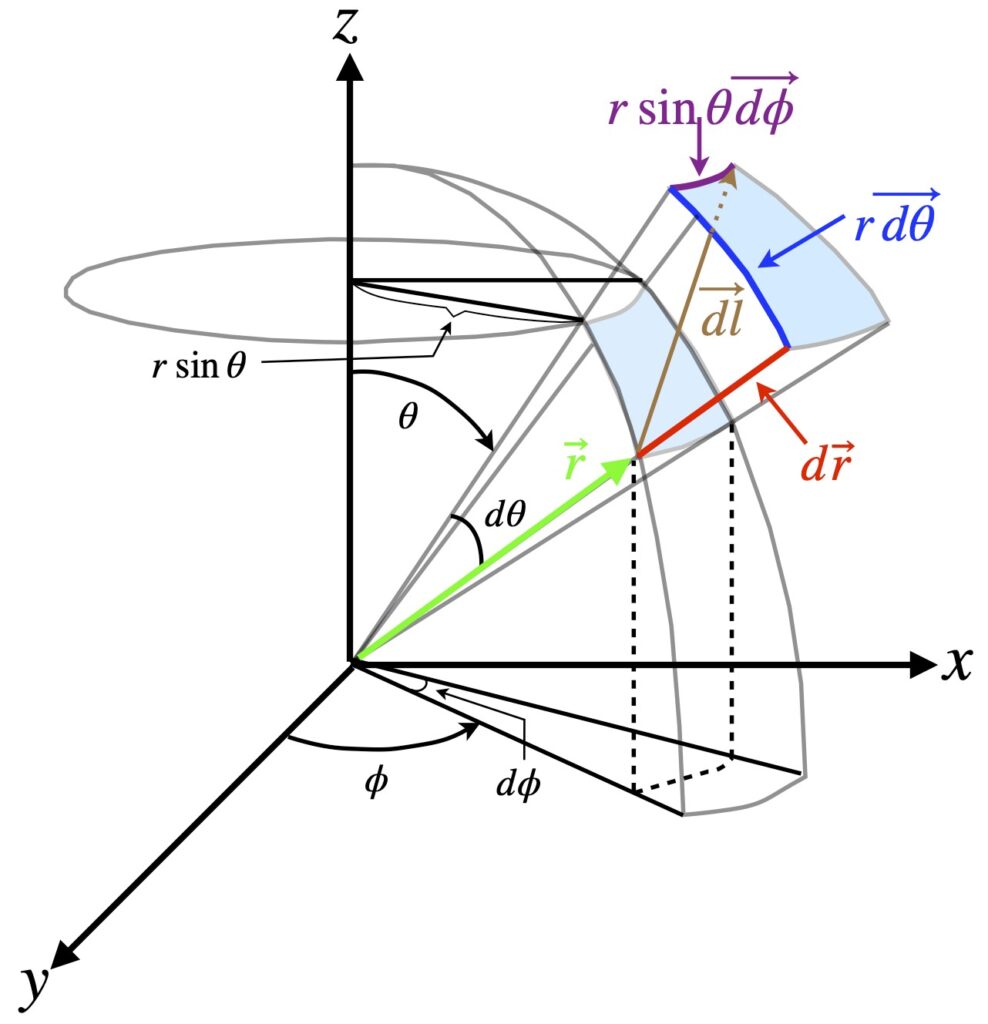
Figure X (obviously not drawn to scale) shows an infinitesimal spherical volume element. But that’s not what we’re actually interested in here. What we’re interested in is $\vec{dl}$ (colored brown in the diagram). It represents an infinitesimal displacement made from:

An infinitesimal displacement in the radial direction with magnitude 1 (shown in red)
An infinitesimal displacement in the 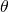$\theta$ direction with magnitude $r$ (shown in blue)
An infinitesimal displacement in the 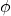$\phi$ direction with magnitude 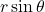$r\sin\theta$ (shown in purple)

We obtain the magnitude of the $\theta$ -direction infinitesimal vector by recognizing that that vector is a tiny arc on a sphere. In general, the length of an arc is given by the radius of the sphere times the angle subtended by the arc in radians. In the case of the $\theta$ -direction vector, the radius is $r$ and the angle subtended by the arc is $d\theta$ .

Similarly, the magnitude of the $\phi$ -direction infinitesimal vector is given by the radius, $r\sin\theta$ (derived above), times the magnitude of the angle in the $\phi$ direction, $d\phi$ .

Thus, we can express the infinitesimal displacement vector, $\vec{dl}$ as:

$\vec{dl} = \vec{dr} +r \vec{d\theta} + r\sin\theta\vec{d\phi}$

The length of $\vec{dl}$ – which, by definition, is the line element $ds^2$ – is arrived at by taking the dot product of $\vec{dl}$ with itself:

$ds^2 = \vec{dl} \cdot \vec{dl}$
$= (\vec{dr} +r \vec{d\theta} + r\sin\theta\vec{d\phi}) \cdot (\vec{dr} +r \vec{d\theta} + r\sin\theta\vec{d\phi})$
$=dr^2 + r^2\,d\theta^2 + r^2\sin^2\,d\phi^2$

Vector Components in Rotated Cartesian Coordinates

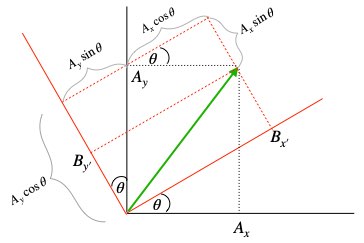
Components in A and B coordinates:
$\vec{A}=(A_x,A_y)$
$\vec{B}=(B_{x^{\prime}},B_{y^{\prime}})$

From the diagram, we can see that:
$B_{x^{\prime}}=A_y\sin\theta+A_x\cos\theta$
$B_{y^{\prime}}=A_y\cos\theta-A_x\sin\theta$

Rearrange:
$B_{x^{\prime}}=\,\,\,\,\,\cos\theta A_x+\sin\theta A_y$
$B_{y^{\prime}}=-\sin\theta A_x+\cos\theta A_y$

Write the above equation in matrix form:

$\displaystyle \begin{bmatrix}B_{x^{\prime}}\\B_{y^{\prime}}\end{bmatrix}=\begin{bmatrix}\,\,\,\,\cos\theta&\sin\theta\\-\sin\theta&\cos\theta\end{bmatrix}=\begin{bmatrix}A_x\\A_y\end{bmatrix}$

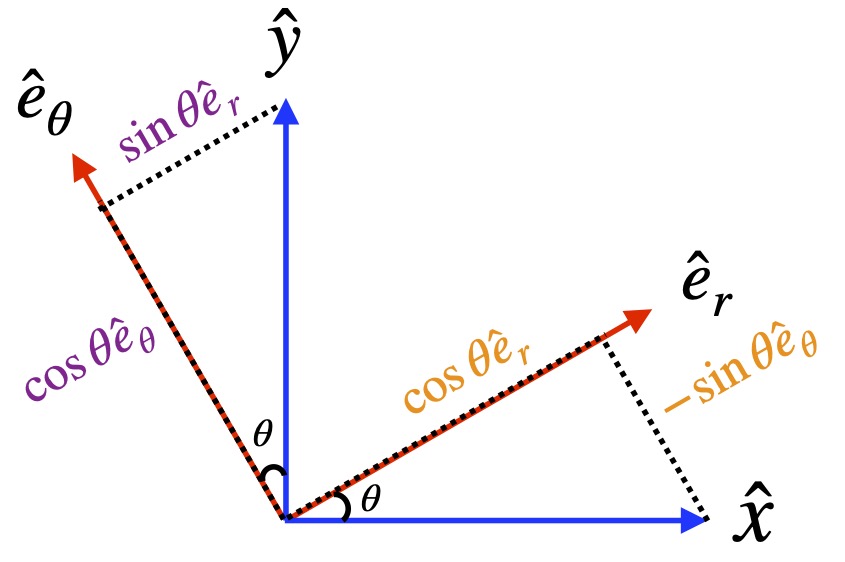
Basis vector rotation in Cartesian coordinates

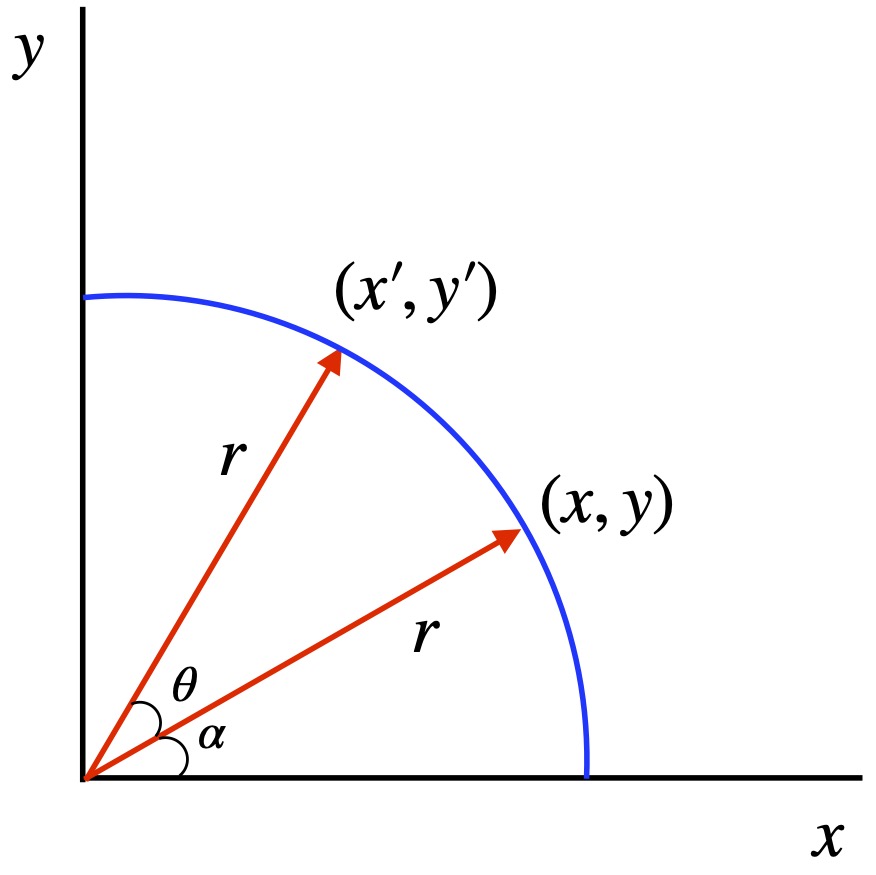
Coordinate transformation for rotated vector

$x = r \cos \alpha$
$x = r \sin \alpha$

and

$x^{\prime} = r \cos (\theta + \alpha)$
$y^{\prime} = r \sin (\theta + \alpha)$

Using the appropriate trigonometric identities, we have:

$\begin{align*} x^{\prime} &= r (\cos \alpha \cos \theta - \sin \alpha \sin \theta)\\ &= r\cos \theta \cos \alpha - r\sin \theta \sin \alpha\\ &= (r\cos \alpha)\cos \theta - (r\sin \alpha) \sin \theta \\ &= x \cos \theta - y \sin \theta \end{align*}$

$\begin{align*} y^{\prime} &= r (\sin \alpha \cos \theta - \cos \alpha \sin \theta)\\ &= r\sin \alpha \cos \theta + r\cos \alpha \sin \theta\\ &= (r\sin \alpha) \cos \theta + (r\cos \alpha) \sin \theta\\ &= y \cos \theta + x \sin \theta \end{align*}$

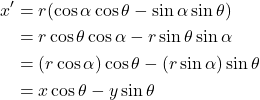
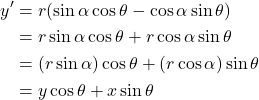
In matrix form:

$\displaystyle \begin{bmatrix} x^{\prime}\\y^{\prime} \end{bmatrix} = \begin{bmatrix}\cos \theta & -\sin \theta\\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix}$

Table of Contents