Contents
- Euclid’s Postulates
- Supplementary Angles
- Complementary Angles
- Vertical Angles
- Area of a Rectangle
- Area of a Triangle
- Pythagorean Theorem
- Corresponding and Alternate angles
- Sum of the Angles of a Triangle
Euclid’s Postulates
Postulate 1
Given two points, A and B, there is a straight line segment, AB, that has them as endpoints.
Postulate 2
Any straight line segment can be extended indefinitely in a straight line.
Postulate 3
Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
Postulate 4
All Right Angles are congruent (i.e., they have the same value).
Postulate 5
If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two Right Angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the Parallel Postulate.
Supplementary Angles
Angles a and b (abbreviated ![]() and
and ![]() ) are supplementary if they add up to
) are supplementary if they add up to ![]() radians, also called a straight angle).
radians, also called a straight angle).
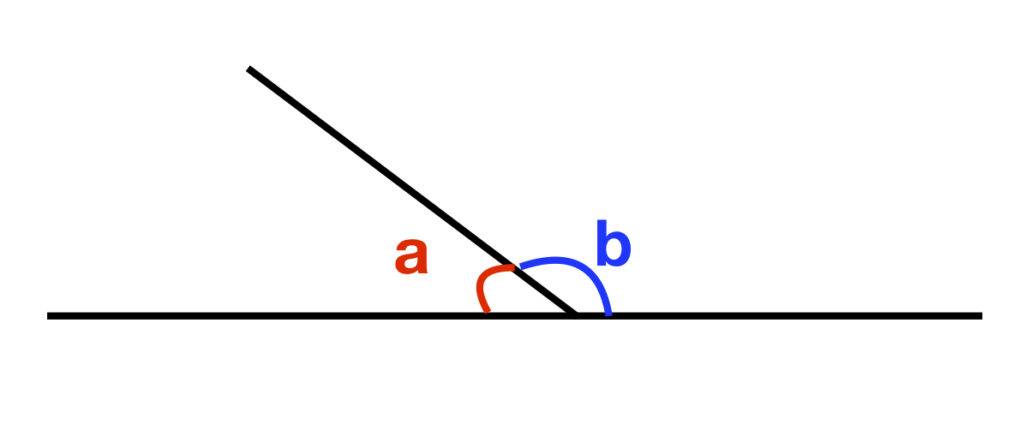
Complementary Angles
Angles are complementary if they add up to ![]() .
.
Vertical Angles
Given two intersecting lines, the two nonadjacent angles with the same vertex are said to be vertical angles.
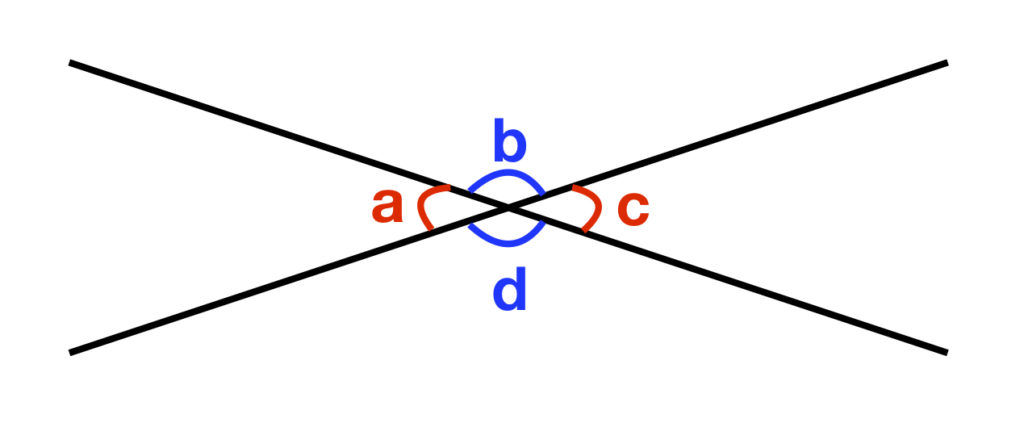
In figure 2, ![]() and
and ![]() are vertical angles. So are
are vertical angles. So are ![]() and
and ![]() .
.
By the definition of supplementary angles,
![]()
![]()
That means that
![]()
Subtract ![]() from both sides of the equation:
from both sides of the equation:
![]()
So ![]() and
and ![]() are congruent. You could make a similar argument to show that
are congruent. You could make a similar argument to show that ![]() . This proves that vertical angles, in general, are congruent.
. This proves that vertical angles, in general, are congruent.
Area of a Rectangle
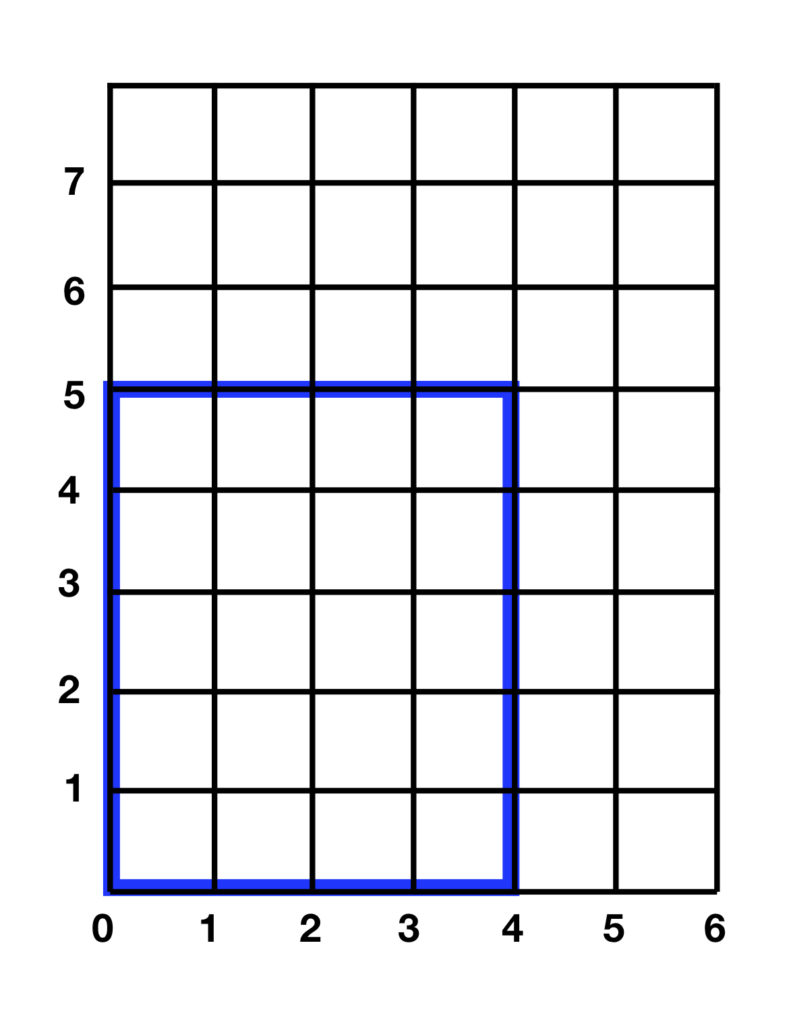
The area of a rectangle equals width times height.
A = w x h
This is easy to see from figure 3. In the figure, the height of the blue rectangle is 5 units and the width is 4 units. Each row of this rectangle contains 4 units of length and there are 5 such rows. 5 x 4 = 20.
Area of a Triangle
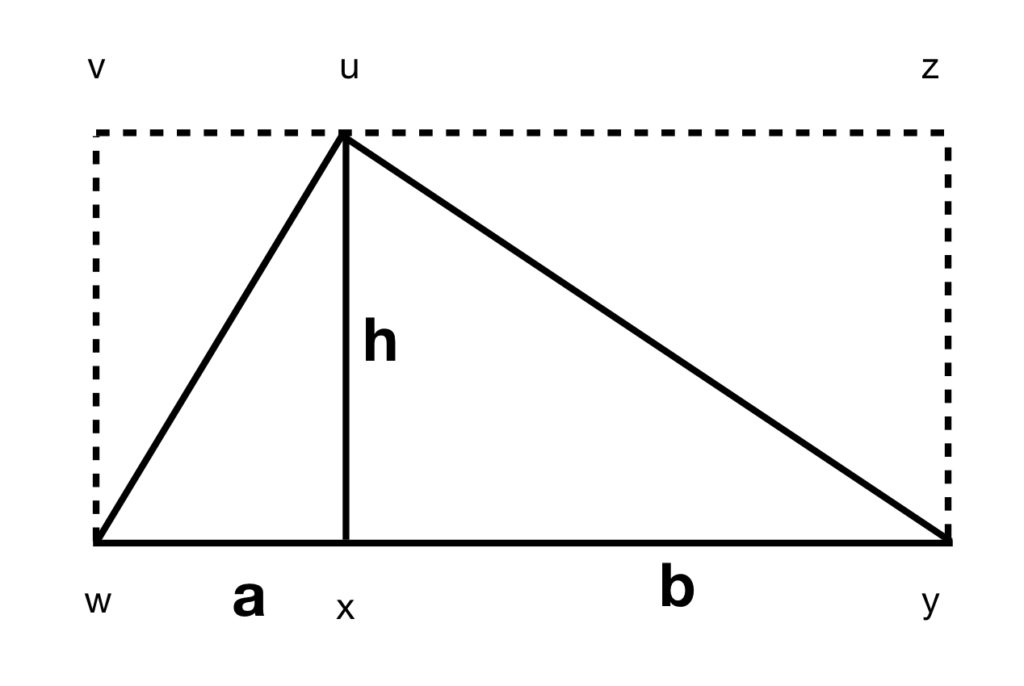
The area of a triangle is given by
![]()
Here is the proof. Referring to figure 4:
- The area of the rectangle vwxu equals its height, h, times its width, a:
 .
. - The line segment uw divides
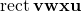 in half; therefore, the area of the smaller triangle on the left,
in half; therefore, the area of the smaller triangle on the left, 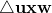 , equals
, equals 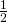 times the area of
times the area of 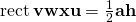 .
. - The area of rectangle uxzy equals its height, h, times its width, b:
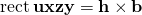 .
. - The line segment uy divides
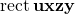 in half; therefore, the area of the larger triangle on the left,
in half; therefore, the area of the larger triangle on the left, 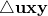 , equals
, equals 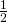 times the area of
times the area of 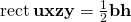 .
. - The triangle whose area we ultimately wish to find,
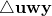 , equals the area of the smaller left and larger right triangles added together:
, equals the area of the smaller left and larger right triangles added together:
![]()
Pythagorean Theorem
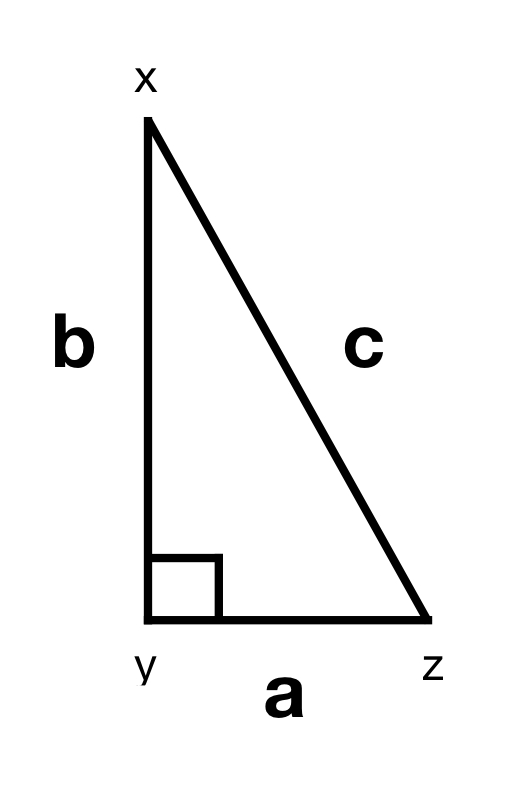
In figure 3, ![]() is a right angle-
is a right angle-![]() . Then the triangle in the figure is a right triangle (a triangle in which one of its angles is a right angle). In a right triangle, the side opposite the right angle (in the above diagram, c) is called the hypotenuse. The Pythagorean theorem states:
. Then the triangle in the figure is a right triangle (a triangle in which one of its angles is a right angle). In a right triangle, the side opposite the right angle (in the above diagram, c) is called the hypotenuse. The Pythagorean theorem states:
For any right triangle, the sum of the squares of the sides adjacent to the right angle equals the square of the hypotenuse.
Mathematically,
![]()
There are several proofs of the Pythagorean theorem. The following link shows 3 of these:
http://jwilson.coe.uga.edu/emat6680/brown/6690/pythathm.htm
We will examine one of these proofs here.
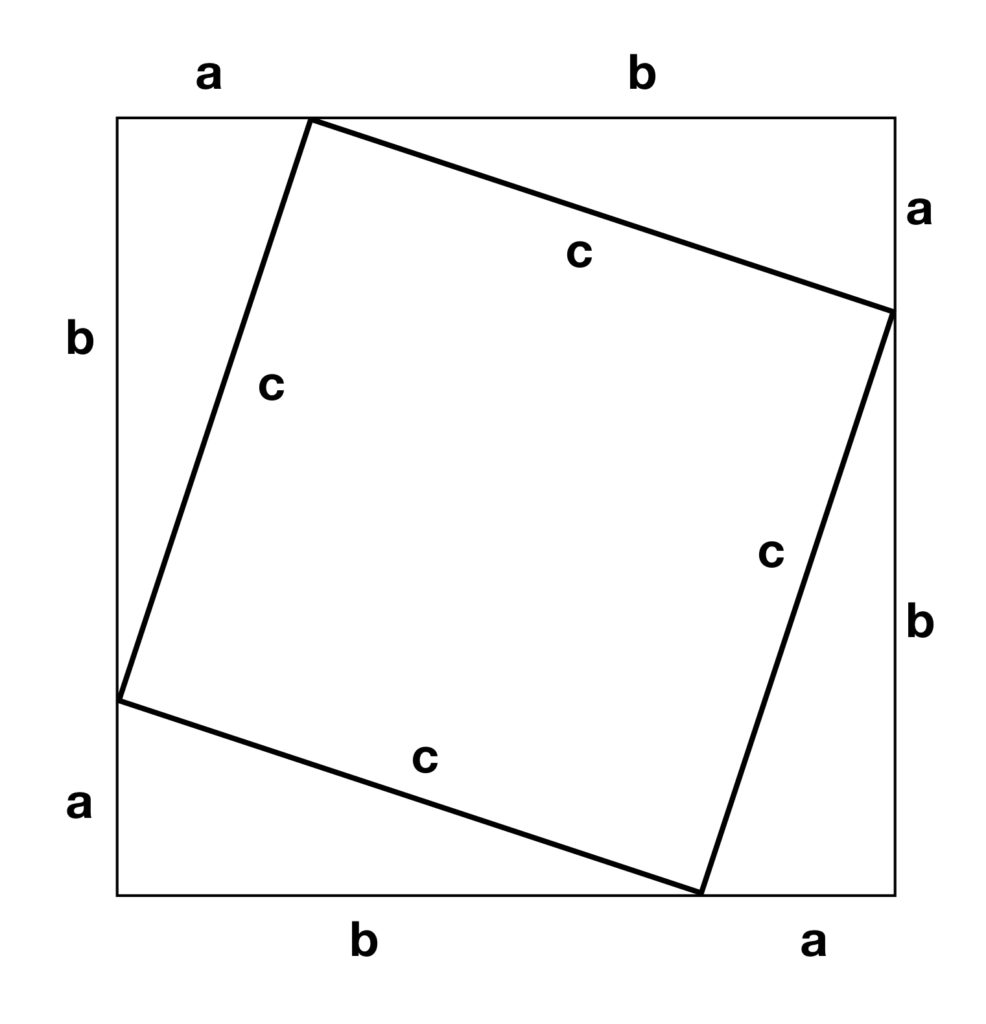
In figure 4,
- There is a large square that contains a smaller square.
- The length of each side of this large square is
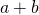 .
. - The area of this large square equals its height times its width. Since its height and width are the same, then its area equals the length of a side squared:
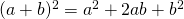 .
. - But the area of this large square can also be expressed as the sum of the area of the 4 triangles and one smaller square it contains.
- Specifically, the area of each of the small triangles is
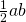 . There are 4 of them so the area contributed by the triangles to the area of the large square is
. There are 4 of them so the area contributed by the triangles to the area of the large square is 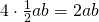 .
. - The area contributed by the small square inside the larger square equals the length of one of its sides squared, in this case,
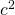 .
. - The total area of the large square must equal the sum of the areas of its parts. Therefore, we have
![]()
So,
![]()
That is what we sought to prove.
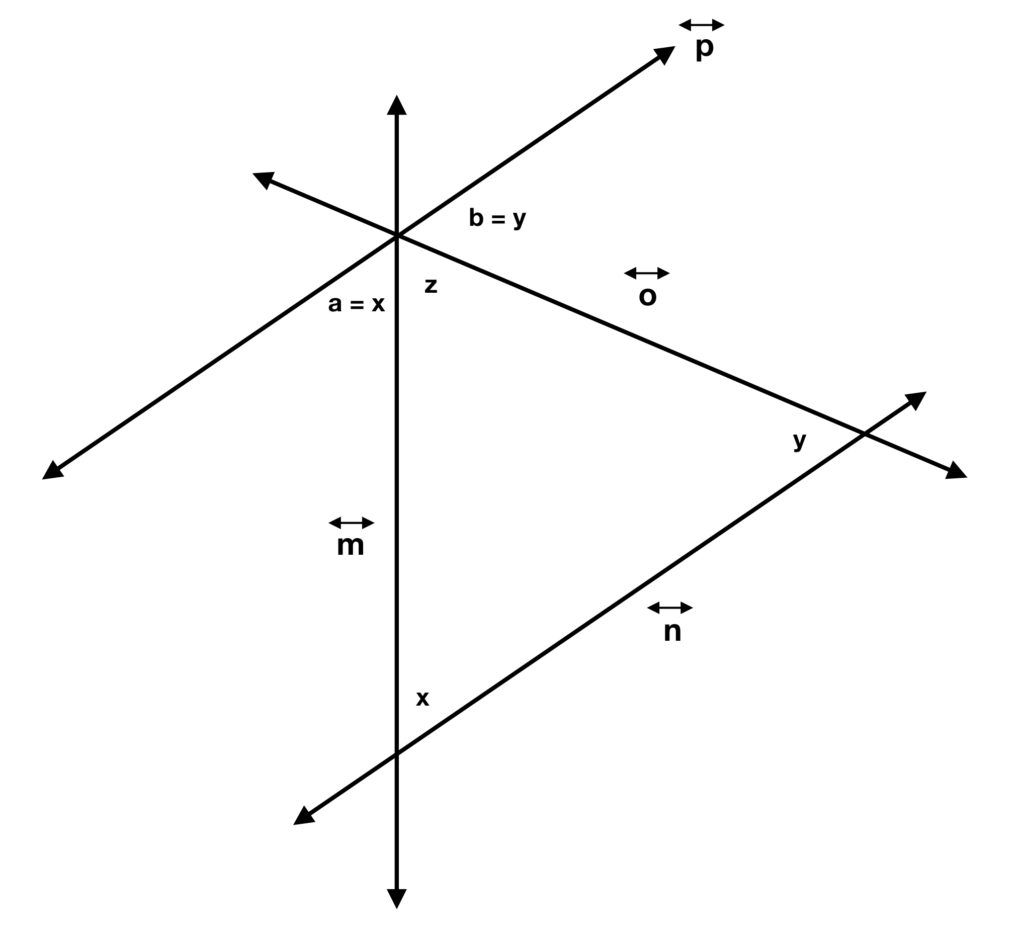
Corresponding and alternate angles
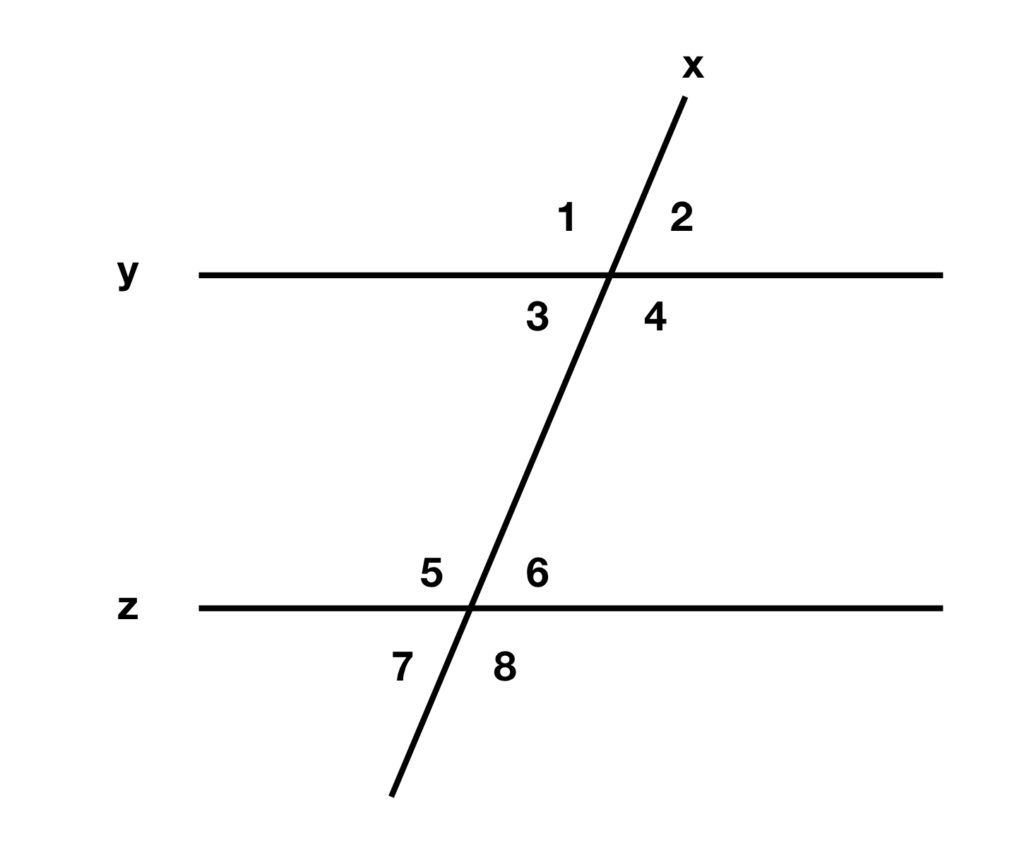
In figure 5, y and z are parallel lines and x is called a traversal line.
Since y and z are parallel, if you drop a perpendicular line segment between the parallel lines, the distance of that perpendicular line segment at every set of points is equal. Now translate all points of the line segement y toward z in the direction of those perpendicular line segments, at the same rate (so the line segment remains oriented at the same angle). When y reaches z,
 overlaps
overlaps 
 overlaps
overlaps 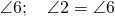
 overlaps
overlaps 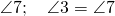
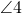 overlaps
overlaps 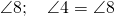 .
.
Angles that are equal to each other are referred to as congruent angles. These angles that become congruent by this translation process are called corresponding angles.
Furthermore, be definition:
- The angles between y and z (
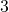 ,
, 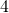 ,
, 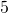 and
and 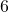 ) are called internal angles.
) are called internal angles. - The angles above y and below z (
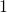 ,
, 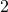 ,
, 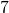 and
and 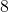 ) are called external angles.
) are called external angles. - Alternate angles are those on different sides of the traversal line.
Using the derivation of vertical angle congruence described above, the following theorems can be proven:
- Alternate internal angles are congruent (i.e., are equal):
- Alternate external angles are congruent:
An example of such a proof goes something like this:
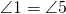
- Using the vertical angle congruence theorem,
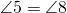
- Therefore,
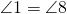
A nice summary of the above information can be found at:
https://mathbitsnotebook.com/Geometry/ParallelPerp/PPangles.html
The Sum of the Angles of a Triangle equals 180º
In figure 6,
- We have a triangle constructed by 3 lines:
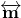 ,
, 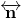 and
and 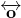 .
. - The triangle contains angles
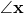 ,
, 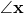 and
and 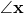 .
. 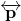 is a line that is parallel to
is a line that is parallel to 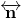 and which intersects the intersection of lines
and which intersects the intersection of lines 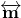 and
and 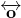 .
.
By the definition of supplementary angles:
![]()
However,
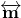 is a traversal of parallel lines,
is a traversal of parallel lines, 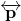 and
and 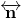 .
.- That makes
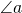 and
and 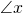 alternate internal angles. From our discussion above, it is known that alternate internal angles are congruent. Thus,
alternate internal angles. From our discussion above, it is known that alternate internal angles are congruent. Thus, 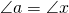 .
. - It also makes
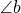 and
and 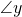 alternate internal angles. Therefore,
alternate internal angles. Therefore, 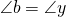 .
.
Given that
It follows that
![]()
which is what we hoped to prove.
