Hyperbolic Trigonometry

This page represents some notes designed to provide the basics of hyperbolic functions.

Table of Contents

Overview

HyperbolicTrigDownload

Hyperbolic Sine of Sum

The following proof is taken from:

https://proofwiki.org/wiki/Hyperbolic_Sine_of_Sum

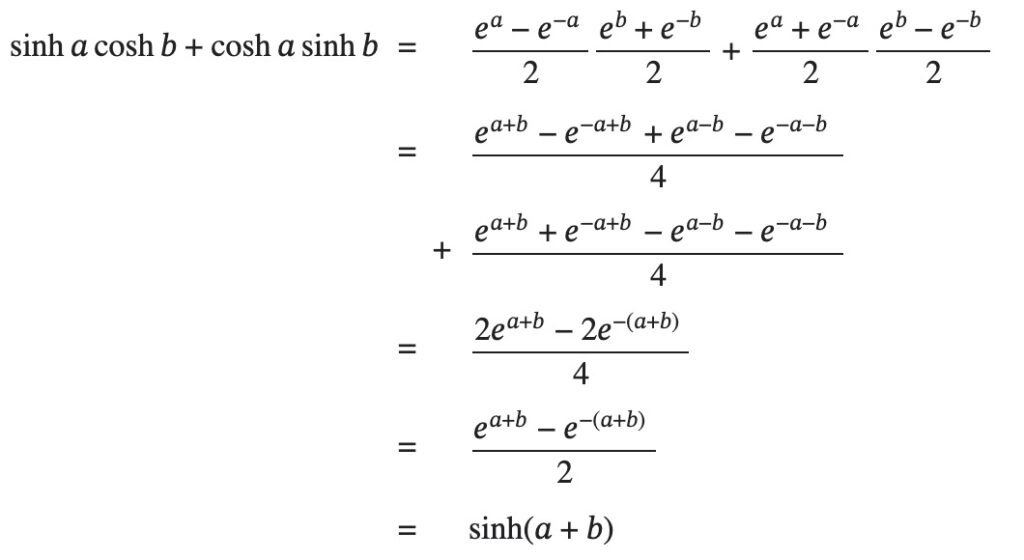
Sinh of sum proof

It can also be proven that \sinh\,a\cosh\,b - \cosh\,a\sinh\,b=\sinh(a-b) by replacing \displaystyle \frac{e^a+e^b}{2} \displaystyle \frac{e^a-e^b}{2} with -\displaystyle \frac{e^a+e^b}{2} \displaystyle \frac{e^a-e^b}{2}.

Hyperbolic Cosine of Sum

The following proof is taken from wikiproof.org:

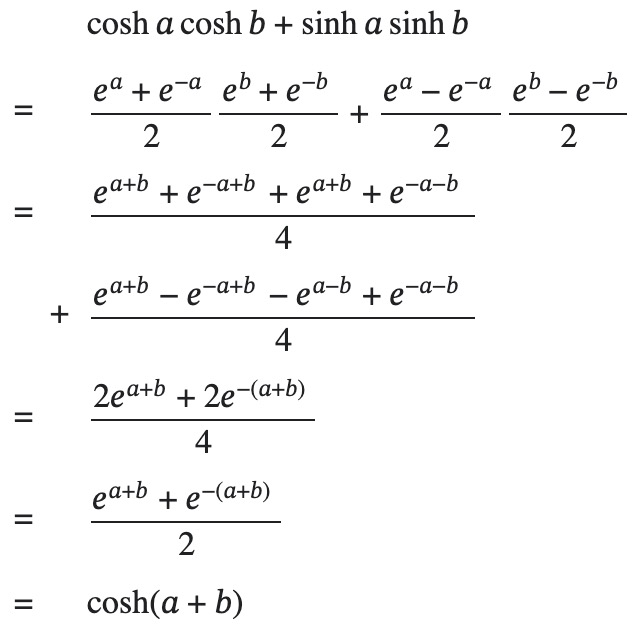
Hypertrophic cosine of sum proof

As is the case for the sinh sum formula, one can prove that \cosh\,a\cosh\,b - \sinh\,a\sinh\,b=\cosh(a-b) by replacing \displaystyle \frac{e^a-e^{-a}}{2} \displaystyle \frac{e^b-e^{-b}}{2} with \displaystyle -\frac{e^a-e^{-a}}{2} \displaystyle \frac{e^b-e^{-b}}{2}.

Hyperbolic Tangent of Sum

This proof is taken from wikiproof.org.

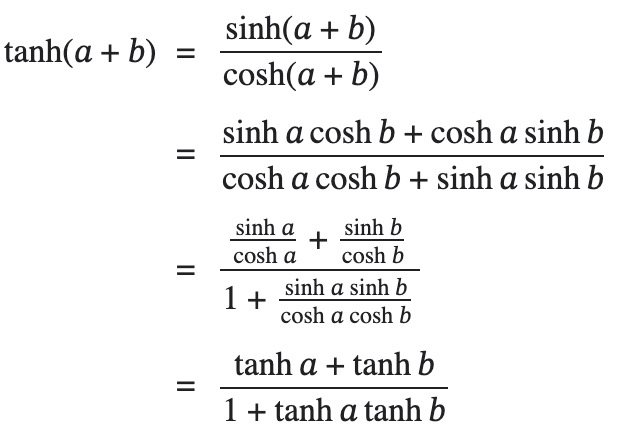
Hyperbolic tangent of sum proof

Similar to the previous proofs, we can show that:

    \[ \tanh(a-b) = \displaystyle \frac{\tanh\,a + \tanh\,b}{1 + \tanh\,a \tanh\,b} \]

by substituting \sinh(a-b) for \sinh(a+b) and \cosh(a-b) for \cosh(a+b) in the above proof.