A third formulation of classical mechanics that is equivalent to Newtonian mechanics and derivable from Hamiltonian and Lagrangian mechanics is the Hamilton-Jacobi formulation. It relates the action, ![]() , to some of the other quantities described in Hamiltonian mechanics. It is also the classical theory with closest similarities to quantum mechanics. Derivation of the equations of this theory is largely taken from the following source:
, to some of the other quantities described in Hamiltonian mechanics. It is also the classical theory with closest similarities to quantum mechanics. Derivation of the equations of this theory is largely taken from the following source:
http://galileoandeinstein.physics.virginia.edu/7010/CM_08_ActionEndPts.html
We know from our derivation of the least action principle that, after integration by parts, we are left with
(1) 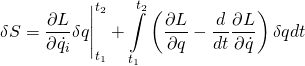
The second term on the right side, 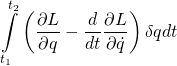 , contains the expression that results from the principle of stationary action –
, contains the expression that results from the principle of stationary action – ![]() . This expression equals zero so we can ignore it. That leaves us with
. This expression equals zero so we can ignore it. That leaves us with
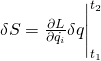
Now keep the spatial starting points and the starting and ending times of the configuration space trajectory the same but vary the spatial end point (which we’ll designate ![]() ) infinitesimally. We get:
) infinitesimally. We get:
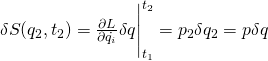
If we add up all of the little infinitesimal changes, we get the total change and we can drop the subscripts.
![]() where
where ![]() is very small. Divide both sides of this equation by
is very small. Divide both sides of this equation by ![]() .
.
Take the limit as ![]() goes to zero of this last equation:
goes to zero of this last equation:
(2) ![]()
Now let’s vary the time of the endpoint ![]() infinitesimally to
infinitesimally to ![]() . That changes the path of the action slightly. Next, find the total derivative of the action (which is a function of position and time) with respect to time. This equals:
. That changes the path of the action slightly. Next, find the total derivative of the action (which is a function of position and time) with respect to time. This equals:
![]()
![]()
![]()
From the result we just obtained above, ![]() . This leads to
. This leads to
![]()
![]()
![]()
By the definition of the Hamiltonian
![]()
Thus,
![]()
![]()
![]()
Recall that 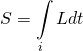 . By the fundamental theorem of calculus,
. By the fundamental theorem of calculus, ![]() . Therefore,
. Therefore,
![]()
![]()
![]() becomes
becomes
![]()
![]()
![]()
Subtracting ![]() from both sides, we get
from both sides, we get
(3) ![]()
Equation 3 is called the Hamilton-Jacobi equation.
