This discussion is adapted from the following reference:
Susskind, L. and Hrabovsky, G. (2014). The Theoretical Minimum: What You Need to Know to Start Doing Physics. 1st ed. Basic Books, pp. 148-160.
It can be found here.
We introduced, in a separate article, the concept of the Lagrangian. Suppose we want to see how the Lagrangian evolves with time. This can be expressed mathematically as follows:
(1) ![]()
The Lagrangian above has no explicit dependence on time. However, there is nothing to say that this has to be the case. If we examine the time evolution of a Lagrangian with time dependence, equation 1 becomes:
(2) ![]()
Let’s look at the terms on the right-hand side of the equation individually. First, terms in the Lagrangian that depend on the partial derivative of ![]() involve the derivative of the potential energy which is equal to the negative of force. Force, in turn, is the derivative of the canonical momentum,
involve the derivative of the potential energy which is equal to the negative of force. Force, in turn, is the derivative of the canonical momentum, ![]() . For example, for the Lagrangian we’ve been working with,
. For example, for the Lagrangian we’ve been working with, ![]() ,
, ![]() . Thus,
. Thus,
![]()
In the second term on the right-hand side, ![]() , the only term in the Lagrangian that depends on
, the only term in the Lagrangian that depends on ![]() is the kinetic energy term,
is the kinetic energy term, ![]() . Therefore,
. Therefore,
![]()
and
![]()
Combining the above equations, we get
![]()
By the the product rule of derivatives, the first two terms on the right side of the above equation can be simplified:
![]()
Thus, we’re left with
(3) ![]()
Next, define a new quantity called the Hamiltonian. Represent it mathematically by ![]() . Define it as follows:
. Define it as follows:
(4) ![]()
That means that ![]() . Substitute this into equation 3:
. Substitute this into equation 3:
![]()
![]()
![]()
![]()
(5) ![]()
What this indicates is that, if the Lagrangian contains a term or terms that are dependent on time, then the Hamiltonian varies with time. On the other hand, if the Lagrangian does not contain a term or terms that depend explicitly on time, then ![]() and
and ![]() . That means that the the Hamiltonian does not change with time, which means that it’s constant, which means that it’s a so-called conserved quantity.
. That means that the the Hamiltonian does not change with time, which means that it’s constant, which means that it’s a so-called conserved quantity.
But what actually is the Hamiltonian. This next series of equations will make it’s nature clear.
To see this best, let’s return to our simple Lagrangian associated with a single particle moving through a potential energy field in one direction, the ![]() -direction:
-direction: ![]()
Recall that the momentum is given by ![]() .
.
Substituting these values into equation 4, we have
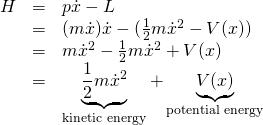
But kinetic energy + potential energy equals the total kinetic energy of a system. Thus, the Hamiltonian represents the total energy of a system.
That the Hamiltonian represents the total energy of a system, in and of itself, is an important fact. However, its importance in physics ranges even further than this. Namely, its equations are functions of ![]() , the momentum and
, the momentum and ![]() , position in space. This is in contradistinction to the Lagrangian formulation of classical physics which deals with functions of
, position in space. This is in contradistinction to the Lagrangian formulation of classical physics which deals with functions of ![]() only. The former leads to first-order differential equations, which are generally easier to solve, as opposed to the Lagrangian formulation which involves second-order differential equation. Also, because the Hamiltonian mechanics utilizes functions of momentum and position, it deals with phase space – a plot of position versus momentum – as opposed to Lagrangian physics, which utilizes configuration space – a plot of position versus time. Both yield the same results, results which agree with the Newtonian physics. They just approach the issues of classical physics from different angles.
only. The former leads to first-order differential equations, which are generally easier to solve, as opposed to the Lagrangian formulation which involves second-order differential equation. Also, because the Hamiltonian mechanics utilizes functions of momentum and position, it deals with phase space – a plot of position versus momentum – as opposed to Lagrangian physics, which utilizes configuration space – a plot of position versus time. Both yield the same results, results which agree with the Newtonian physics. They just approach the issues of classical physics from different angles.
Indeed, just as there are distinctive equations that characterize Newtonian mechanics and Lagrangian physics, the Hamilton formulation of classical physics is marked by characteristic equations of motion. We will derive them now. We’ll follow the lead of Dr. Susskind’s book and start with an intuitive argument involving one particle affected by a potential energy field moving in only one dimension.
We start with two equations:
![]()
![]()
Replace velocity with ![]() . We get
. We get
![]()
Take the partial derivative of both sides with respect to ![]() . The only term that depends on
. The only term that depends on ![]() on the right side of this equation is
on the right side of this equation is ![]() . So,
. So,
![]() which equals
which equals
![]()
Therefore,
(6) ![]()
This is the first of the so-called Hamilton’s equations.
To derive the second, take the partial derivative of ![]() with respect to
with respect to ![]() , the momentum:
, the momentum:
![]()
But ![]() . Thus,
. Thus,
(7) ![]()
This is the second of Hamilton’s equations.
Here is the general derivation. Consider the Lagrangian written in terms of general coordinates:
![]()
The Hamiltonian is
![]()
Now make an infinitesimal change (denoted by ![]() ) in
) in ![]() :
:
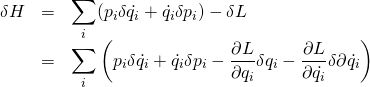
From Lagrangian mechanics, we have ![]() . We this expression into the first term of the equation above giving us
. We this expression into the first term of the equation above giving us ![]() . This term cancels out with the fourth term in the above equation leaving us with:
. This term cancels out with the fourth term in the above equation leaving us with:
![]()
Let’s develop an expression for an infinitesimal change in ![]() and compare it to this last equation:
and compare it to this last equation:
![]()
Comparison of these two equations reveals that:
(8) ![]()
and
(9) ![]()
From Lagrangian mechanics, we know that ![]() . Therefore,
. Therefore,
(10) ![]()
