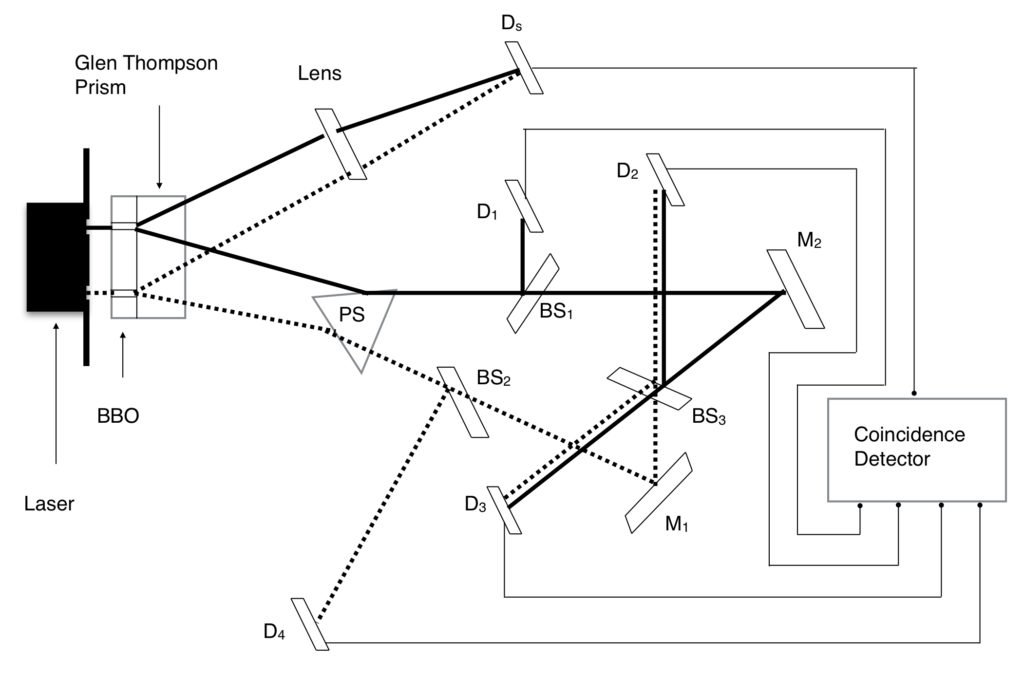
We start with an argon laser and we fire single 351 nanometer wavelength photons at a double-slit screen. The photons go through both slits through a nonlinear beta barium borate crystal which creates pairs of entangled photons each with half the energy (i.e. twice the wavelength, 702.2 nanometers) as the original photon. The possible paths of photons traveling through the upper slit are coded by a solid black line; those traveling through the upper slit are coded by a dotted line. Each pair of entangled photons are then deflected by a Glen-Thompson prism either upward to detector Ds or downward to another prism, PS. At prism PS, the upper (solid) photons will be directed to a beam splitter, BS1, and the lower (dotted) photons will be directed to a second beam splitter, BS2. Photons that go to detector Ds are called signal photons; those that go to PS are called idler photons.
At BS1, half of the photons, originally from the upper (solid) source, will be deflected upward to detector D1 while the other half will pass through to mirror M2. Similarly, at BS2, half of the photons, originally from the lower (dotted) source, will be deflected downward to detector D4 while the other half will pass through to mirror M1.
If only detector Ds were present (no prism PS), then signal photons from upper (solid) and lower (dotted) slits would hit the Ds and an interference pattern would be created. However, with all the other elements in place, a single, wide band appears on Ds. Why? We’ll delve into that more, later.
Consider, first, what patterns emerge at detectors D2 and D1. If an idler photon hits D1, there’s only one way it could have gotten there—from the upper slit, along the upper path. Likewise, if an idler photon hits D4, there’s only one way it could have gotten there—from the lower slit, along the dotted path. So single, narrow bands are seen on detectors D4 and D1. Note that if a photon hits one of these detectors, it imparts specific information about which path the photon took to an observer (i.e., the experimenter). And because it’s entangled with its corresponding signal photon, as we’ll see, it influences the behavior of the signal photon.
Next consider what happens if an idler photon passes through prism PS and beam splitters BS1 and BS2. Well, whether they follow the solid path or the dotted path, they get reflected off of mirrors and end up at a third beam splitter, BS3. If a photon enters BS3 from the solid path, it can either pass through to detector D3 or be deflected to D2. If it enters BS3 from the dotted path, it can either be deflected to detector D3 or pass through to D2. Either way, photons hitting detectors D2 and D3 can get to that detector either along the solid pathway or the dotted pathway. Because there’s no way to tell from which slit a photon hitting detectors D2 and D3 came, an interference pattern builds up on both of these detectors.
Because entangled photon pairs are emitted at the same time, we can correlate the behavior of photons that hit Ds with photons that hit detector D1, D2, D3 or D4 at about the same time. We can do this with a coincidence detector, which works as follows: when a photon hits a detector, it sends an electronic signal over a wire to the coincidence detector. If photons hit detectors Ds and D1 in close temporal proximity, the coincidence detector plots the position where the photon hit the Ds detector, onto a graph called R1. If Ds and D2 register hits on the coincidence detector close together in time, then the Ds position is plotted on a graph called R2. Similarly, near simultaneous coincidence registration from Ds-D3 and Ds-D4 plot the position of the corresponding Ds hit onto graphs labeled R3 and R4, respectively. This is how the experimental setup teases out the possible relationships between the behavior of signal photons and the behavior of the various types of idler photons from the otherwise amorphous blob of signal that’s found on the Ds detector.
And what do we find after this analysis is performed? We find that the R1 and R4 graphs show single peaks and the R2 and R3 graphs show interference patterns. R1 and R4 show single peaks because, as alluded to just a minute ago, if the idler photon hits either D1 or D4 (to help create the R1 and R4 maps) then an observer analyzing the data knows exactly which path the photon followed. This is tantamount to the experimenter observing the photon. Some physicists have suggested that the reason that the wave function collapses and a classical pattern (instead of an interference pattern) appears on a detector in the simple double slit experiment is because the act of observation somehow disturbs the photon. From this experiment, though, it’s clear that this can’t be the case since nothing interacts with the signal photons on their way to the Ds detector.
What about R2 and R3? Well, activation of the D2 and D3 detectors in close temporal proximity to Ds activation is what makes the R2 and R3 maps. Because both upper (solid) and lower (dotted) photons contribute to the interference pattern seen at D2 and D3, and the experimenter (observer) doesn’t know which path the photons took to get to those detectors, just like in the simple double slit experiment without an observer, an interference pattern is seen at Ds. It seems, then, that the thing that determines what pattern the photons make on the Ds detector is whether or not the experimenter (observer) has knowledge of which path entangled idler photons take.
But here’s the enigma. Photons all move at the same speed – the speed of light. The time it takes to travel some distance is 
(in terms of units, we have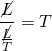 
. From these equations, it’s easy to see that if 1) two particles, A and B, are traveling at the same speed 2) particle A travels a short distance, d1, and 3) particle B travels a longer distance, d2, then particle A will reach its target before particle B. In the delayed quantum eraser experiment, the distance from the photon source to photon detector Ds is shorter than the distance from the source to each of detectors D1, D2, D3 and D4. Therefore, each signal photon will reach detector Ds before its idler pair hits its respective detector, detector D1, D2, D3 or D4. Now we said above that it seems that the thing that the pattern made by signal photons depends on (as manifested in R1, R2, R3 and R4) is which detector its idler pair hits. But how can event S (the signal photon hitting detector Ds) depend on event I (its idler pair hitting detector D1, D2, D3 or D4) if event I occurs after event S?
The diagram (modified slightly) and explanation described above are taken from
https://en.wikipedia.org/wiki/Delayed-choice_quantum_eraser
The author is Patrick Edwin Moran.